SG
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 5 2017
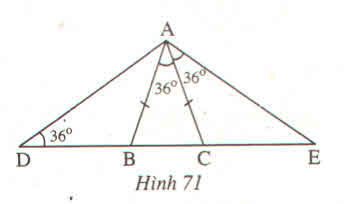
Tam giác ABC có AB = AC (theo đề bài)
Suy ra: tam giác ABC cân tại A( dựa theo định nghĩa tam giác cân)
=> góc ABC = góc ACB ( dựa theo tính chất tam giác cân)
=> góc ABC = góc ACB = \(\left(180^0-36^0\right):2=72^0\)
Có góc ACB + góc ACE = \(180^0\) (2 góc kề bù)
=> góc ACE = \(180^0\)- góc ACB
=> góc ACE = \(180^0-72^0=108^0\)
Tam giác ACE có góc CAE + góc CEA + góc ACE = \(180^0\)(tổng 3 góc của 1 tam giác)
=> góc CEA = \(180^0-\left(108^0+36^0\right)=36^0\)(*)
Tam giác ADE có góc BDA = góc CEA = \(36^0\)
=> tam giác ADE cân tại A ( dựa theo tính chất của tam giác cân)
20 tháng 4 2017
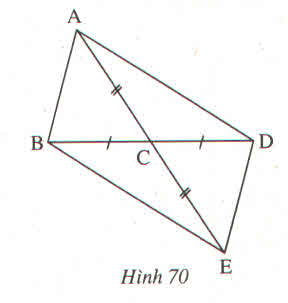
Ta có: ∆AMD=∆AME(Cạnh huyền AM chung, góc nhọn^A1 = ^A2)
∆MDB=∆MEC(Cạnh huyền BM=CM, cạnh góc vuông.
MD=ME, do ∆AMD=∆AME)
∆AMB= ∆AMC(Cạnh AM chung),
Cạnh MB=MC, cạnh AB=AC
Vì AD=AE, DB=EC
LH
20 tháng 4 2017
Ta có: \(\Delta\)AMD=\(\Delta\)AME(Cạnh huyền AM chung, góc nhọn \(\widehat{A}_1=\widehat{A}_2\))
\(\Delta\)MDB=\(\Delta\)MEC(Cạnh huyền BM=CM, cạnh góc vuông )
MD=ME, do \(\Delta\)AMD=\(\Delta\)AME)
\(\Delta\)AMB= \(\Delta\)AMC(Cạnh AM chung),
Cạnh MB=MC, cạnh AB=AC
Vì AD=AE, DB=EC
SG
3
QD
20 tháng 4 2017
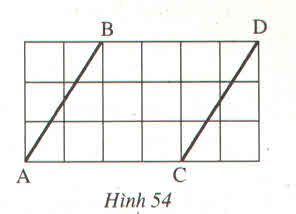
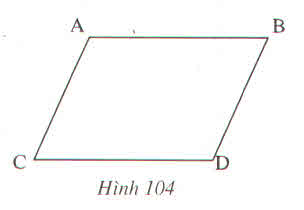
Vẽ đoạn thẳng AD.
∆ADB và ∆DAC có:
ˆA1A1^= ˆD1D1^(so le trong AB//CD)
AD là cạnh chung.
A2^=D2^(So le trong, AC//BD)
Do đó ∆ADB=∆DAC(g.c .g)
Suy ra: AB=CD, BD=AC
Xem thêm tại: http://loigiaihay.com/bai-38-trang-124-sach-giao-khoa-toan-7-tap-1-c42a5073.html#ixzz4elm8F0eT
6 tháng 8 2017
A B C D
Vẽ đoạn thẳng AD.
∆ADB và ∆DAC có:
\(\widehat{A^1}\)= \(\widehat{D^1}\)(so le trong AB//CD)
AD là cạnh chung.
\(\widehat{A^2}\)=\(\widehat{D^2}\)(So le trong, AC//BD)
Do đó ∆ADB=∆DAC(g.c .g)
Suy ra: AB=CD, BD=AC
Giải:
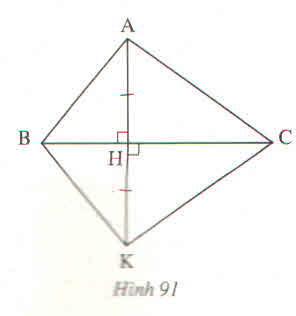
∆AHB và ∆KBH có
AH=KH(gt)
\(\widehat{AHB}\)=\(\widehat{KHM}\)
BH cạnh chung .
nên ∆AHB=∆KBH(c.g.c)
suy ra: \(\widehat{ABH}\)=\(\widehat{KBH}\)
Vậy BH là tia phân giác của góc B.
Tương tự ∆AHC =∆KHC(c.g.c)
Suy ra: \(\widehat{ACH}\)=\(\widehat{KCH}\)
Vậy CH là tia phân giác của góc C.
tam giác KBH nên chuyển thành tam giác KHB