K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
1
SY
15 tháng 3 2016
a) Ta có: 3=1.3=(-1).(-3)
TH1: x+1=1 => x=0 và xy-1=3 => 0y=4.( vô lí)=> loại
TH2: x+1=3 =>x=2 và xy-1=1 => xy=2 => 2y=2 => y=1
TH3: x+1= -1 => x=-2 và xy-1= -3 => xy= -2 => -2y=-2 => y=1
TH4: x+1= -3 => x=-4 và xy-1= -1 => xy=0 Suy ra -4y=0 Suy ra y=0.
Vậy (x,y) thuộc {(2;1); (-2;1) ; (-4;0)}
b) Vì lũy thừa cơ số 6 thì luôn luôn tận cùng là 6 vậy 6666= (...6). Tận cùng=6
KB
0
23 tháng 2 2016
a) Theo đề bài, ta có :
\(\frac{5}{x}-\frac{y}{3}=\frac{1}{6}\) => \(\frac{5}{x}=\frac{1+2y}{6}\)
| 2y+1 | 1 | -1 | 3 | -3 | 5 | -5 | 15 | -15 |
| 2y | 0 | -2 | 2 | -4 | 4 | -6 | 14 | -16 |
| y | 0 | -1 | 1 | -2 | 2 | -3 | 7 | -8 |
| x | 30 | -30 | 10 | -10 | 6 | -6 | 2 | -2 |
b) \(\frac{2}{y}-\frac{x}{6}=\frac{1}{30}\) => \(\frac{2}{y}=\frac{5x-1}{30}\)
| 5x-1 | -1 | 4 | -6 |
| 5x | 0 | 5 | -5 |
| x | 0 | 1 | -1 |
| y | -60 | 15 | -10 |
CM
6 tháng 2 2019
Đáp án C
Phương pháp:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Cách giải:
<=> 
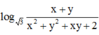
(2)
Đặt 
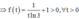
=> f(t) đồng biến trên (0;+∞)
<=> 
<=> 
Khi đó,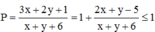 
vì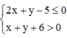 
Vậy Pmax = 1 khi và chỉ khi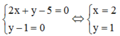 
CM
13 tháng 9 2019
Đáp án C
Phương pháp giải:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Lời giải:
log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y (1)
(2)
Đặt 
=> f(t) đồng biến trên (0;+∞)
Khi đó, 
vì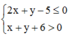 
Vậy Pmax = 1 khi và chỉ khi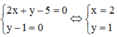 
CM
14 tháng 3 2019
Thay y = 4 x vào biểu thức P và biến đổi ta thu được
P = - 9 log 2 2 + 27 log 2 x - 27 .
Do y ≥ 1 nên x ≤ 4 . Suy ra 1 2 ≤ x ≤ 4 . Đặt t = log 2 x , khi đó - 1 ≤ t ≤ 2 .
Xét hàm số f(t0 = - 9 t 2 + 27t - 27; t ∈ - 1 ; 2
Ta có f ' (t) = -18t + 27; f ' (t) = 0 ⇔ t = 3 2
f (-1) = -63; f (2) = -9; f 3 2 = 27 4
Vậy
m a x P = - 27 4 ⇔ x = 2 2 ; y = 2
Đáp án A
DP
4
9 tháng 4 2016
\(\frac{x}{9}-\frac{3}{y}=\frac{1}{18}\)
<=> \(\frac{xy-27}{9y}\frac{1}{18}\)
<=> \(\frac{2\left(xy-27\right)}{18y}=\frac{y}{18y}\)
=> 2(xy-27) = y
<=> 2xy -27 = y
đến ĐÂY tự giải nha 
thì thử đi
th1:3-x=1;xy+5=-1(-1 chỉ bằng 1nhân-1;-1 nhân1 )
có x rồi thì thế vào xy+5=1 để tìm y
th2 tương tự (tui chỉ gợi ý thui)