Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

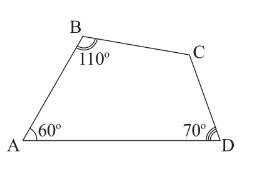
Ta có tổng 4 góc trong tứ giác là: \(360^o\)
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
Hay: \(60^o+110^o+\widehat{C}+70^o=360^o\)
\(\Rightarrow\widehat{C}=360^o-\left(110^o+60^o+70^o\right)120^o\)
Vậy chọn đáp án A

Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 70^\circ + 80^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 30^\circ \end{array}\)
Xét tam giác ABC và tam giác PMN có:
\(\begin{array}{l}\widehat B = \widehat M = 80^\circ \\\widehat C = \widehat N = 30^\circ \end{array}\)
\( \Rightarrow \Delta ABC \backsim \Delta PMN\) (g-g)
\( \Rightarrow \frac{{AB}}{{PM}} = \frac{{BC}}{{MN}} = \frac{{CA}}{{NP}}\) (Tỉ số đồng dạng)

Vì ABCD là hình thang cân
\(\Rightarrow\widehat{A}+\widehat{D}=180^o\)
Nên: \(\widehat{D}=180^o-\widehat{A}=180^o-65^o=115^o\)
Mặt khác ta có ABCD là hình thang cân nên:
\(\widehat{C}=\widehat{D}=115^o\)
Vậy chọn đáp án A

Gọi góc ngoài đỉnh B là x
Ta có:
$\widehat {B} + x = 180^0 $
`=>`$ \widehat {B} + 110^0 = 180^0$
`=>` $\widehat {B} = 70^0$
Xét tứ giác ABCD:
$\widehat {A} + \widehat {B} + \widehat {C} + \widehat {D}= 360^0$
`=>` $100^0 + 70^0 + 75^0 + \widehat {D} = 360^0$
`=>` $\widehat {D} = 115^0$
Vậy, $\widehat {D} = 115^0.$

Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 50^\circ + 60^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 70^\circ \end{array}\)
Xét tam giác ABC và tam giác MNP có:
\(\begin{array}{l}\widehat B = \widehat N = 60^\circ \\\widehat C = \widehat P = 70^\circ \end{array}\)
\( \Rightarrow \Delta ABC \backsim \Delta MNP\) (g-g).

Do ${ABCD}$ là hình thang cân (gt) nên \(\widehat A = \widehat B\)
Xét hình thang \(ABCD\) ta có: \(\widehat {\rm{A}} + \widehat {\rm{B}} + \widehat {\rm{C}} + \widehat {\rm{D}} = 360^\circ \)
\(\begin{array}{l}\widehat A + \widehat B + 75^\circ + 75^\circ = 360^\circ \\\widehat A + \widehat B = 210^\circ \end{array}\)
Mà \(\widehat A = \widehat B\) (cmt)
Suy ra : \(\widehat {\rm{A}} = \widehat B = 105^\circ \)

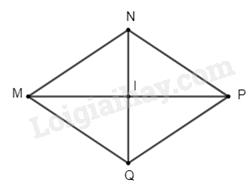
a) Vì \(MNPQ\) là hình thoi (gt)
Suy ra \(IM = IP\) và \(NQ \bot MP\)
Suy ra \(\widehat {{\rm{MIN}}} = 90\)
Xét tam giác vuông \(MPI\) (vuông tại \(I\)) ta có:
\(M{I^2} = M{N^2} - N{I^2} = {10^2} - {6^2} = 100 - 36 = 64\) (định lý Pythagore)
Suy ra \(MI = 8\) (dm)
b) Vì \(MNPQ\) là hình thoi (gt)
Suy ra \(NI\) là phân giác của \(\widehat {MNP}\)
Suy ra \(\widehat {MNI} = \widehat {PNI} = \frac{{128^\circ }}{2} = 64^\circ \)
Xét \(\Delta MNI\) vuông tại \(I\) ta có:
\(\widehat {{\rm{MNI}}} + \widehat {{\rm{NMI}}} = 90\)
Suy ra \(\widehat {IMN} = 90^\circ - \widehat {MNI} = 90^\circ - 64^\circ = 26^\circ \)

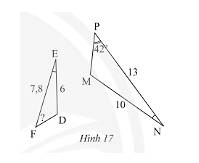
Ta có:
\(\frac{{EF}}{{NP}} = \frac{{7,8}}{{13}} = \frac{3}{5};\frac{{DE}}{{MN}} = \frac{6}{{10}} = \frac{3}{5}\)
Xét tam giác \(DEF\) và tam giác \(MNP\) ta có:
\(\frac{{EF}}{{NP}} = \frac{{DE}}{{MN}} = \frac{3}{5}\)
\(\widehat E = \widehat N\) (giải thuyết)
Do đó, \(\Delta DEF\backsim\Delta MNP\) (c.g.c)
Do đó, \(\widehat F = \widehat P = 42^\circ \).

a) Hình thang \(MNPQ\) có \(\widehat Q = 90^\circ \) nên là hình thang vuông. Suy ra \(\widehat M = 90^\circ \)
Áp dụng định lí tổng các góc của một tứ giác, ta có: \(\widehat P = 360^\circ - \left( {90^\circ + 90^\circ + 125^\circ } \right) = 55^\circ \)
b) Hình thang \(MNPQ\) có \(\widehat P = \widehat Q = 110^\circ \) nên là hình thang cân.
Suy ra \(\widehat M = \widehat N = 180^\circ - 110^\circ = 70^\circ \)