Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(d) qua A(5; 6) : y = mx - 5m + 6 (1)
(C) : (x - 1)² + (y - 2)² = 1 (2)
Thay y từ (1) vào (2) ta có phương trình hoành độ giao điểm của (d) và (C)
(x - 1)² + (mx - 5m + 4)² = 1
Khai triển ra pt bậc 2 : (m² + 1)x² - 2(5m² - 4m + 1)x + 25m² - 40m + 17 = 0 (*)
Để (d) tiếp xúc (C) thì (*) phải có nghiệm kép
∆' = (5m² - 4m + 1)² - (m² + 1)(25m² - 40m + 17) = - 4(3m² - 8m + 4) = 4(m - 2)(2 - 3m) = 0 => m = 3/2; m = 2
KL : Có 2 đường thẳng cần tìm
(d1) : y = (3/2)(x - 1)
(d2) : y = 2x - 4
∆ ∠ ∡ √ ∛ ∜ x² ⁻¹ ∫ π × ∵ ∴ | | , ⊥,∈∝ ≤ ≥− ± , ÷ ° ≠ → ∞, ≡ , ≅ , ∑,∪,¼ , ½ , ¾ , ≈ , [-b ± √(b² - 4ac) ] / 2a Σ Φ Ω α β γ δ ε η θ λ μ π ρ σ τ φ ω ё й½ ⅓ ⅔ ¼ ⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ⁺ ⁻ ⁼ ⁽ ⁾ ⁿ ₁ ₂ ₃₄₅ ₆ ₇ ₈ ₉ ₊ ₋ ₌ ₍ ₎ ∊ ∧ ∏ ∑ ∠ ,∫ ∫ ψ ω Π∮ ∯ ∰ ∇ ∂ • ⇒ ♠ ★

Sử dụng bất đẳng thức AM-GM ta có : \(\left(\frac{1}{a^2}+1\right)\left(\frac{1}{b^2}+2\right)\left(\frac{1}{c^2}+8\right)\ge2\sqrt{\frac{1}{a^2}}.2\sqrt{\frac{2}{b^2}}.2\sqrt{\frac{8}{c^2}}=8.\sqrt{16}.\frac{1}{abc}=\frac{32}{abc}\)
Dấu "=" xảy ra khi và chỉ khi ...
Áp dụng bất đẳng thức cô -si cho 2 số dương , ta có :
\(\hept{\begin{cases}\frac{1}{a^2}+1\ge2\sqrt{\frac{1}{a^2}}=\frac{2}{a}\\\frac{1}{b^2}+2\ge2\sqrt{\frac{1}{b^2}.2}=\frac{2\sqrt{2}}{b}\\\frac{1}{c^2}+8\ge2\sqrt{\frac{1}{c^2}.8}=\frac{4\sqrt{2}}{c}\end{cases}}\)
Nhân vế với vế ts có :
\(\left(\frac{1}{a^2}+1\right)\left(\frac{1}{b^2}+2\right)\left(\frac{1}{c^2}+8\right)\ge\frac{32}{abc}\left(đpcm\right)\)

Ta có \(a+b+c\ge3\sqrt[3]{abc}=3\)
Áp dụng bđt cosi ta có:
\(\frac{a^3}{\left(b+1\right)\left(c+2\right)}+\frac{b+1}{12}+\frac{c+2}{18}\ge3\sqrt[3]{\frac{a^3}{12.18}}=\frac{a}{2}\)
Làm tương tự
=>\(VT+\left(\frac{a+1}{12}+\frac{a+2}{18}\right)+\left(\frac{b+1}{12}+\frac{b+2}{18}\right)+\left(\frac{c+1}{12}+\frac{c+2}{18}\right)\ge\frac{a+b+c}{2}\)
=> \(VT\ge\frac{13}{36}.\left(a+b+c\right)-\frac{7}{12}\ge\frac{13}{36}.3-\frac{7}{12}=\frac{1}{2}\)(ĐPCM)

Đặt: \(\hept{\begin{cases}\frac{1-a}{1+a}=x\\\frac{1-b}{1+b}=y\\\frac{1-c}{1+c}=z\end{cases}}\)
\(\Rightarrow-1< x,y,z< 1\)và \(\hept{\begin{cases}\frac{1-x}{1+x}=a\\\frac{1-y}{1+y}=b\\\frac{1-z}{1+z}=c\end{cases}}\)
Theo đề bài ta có: \(abc=1\Rightarrow\left(1-x\right)\left(1-y\right)\left(1-z\right)=\left(1+x\right)\left(1+y\right)\left(1+z\right)\)
\(\Rightarrow x+y+z+xyz=0\)
Mặt khác ta có: \(\frac{4a}{\left(a+1\right)^2}=1-x^2;\frac{2}{a+1}=1+x\)
Và: \(\frac{4b}{\left(b+1\right)^2}=1-y^2;\frac{2}{b+1}=1+y\)
Và: \(\frac{4c}{\left(c+1\right)^2}=1-z^2;\frac{2}{c+1}=1+z\)
Nên: \(\frac{4a}{\left(a+1\right)^2}+\frac{4b}{\left(b+1\right)^2}+\frac{4c}{\left(c+1\right)^2}\le1+2.\frac{2}{a+1}.\frac{2}{b+1}.\frac{2}{c+1}\)
\(\Leftrightarrow x^2+y^2+z^2+\left(xy+yz+zx\right)+2\left(x+y+z+xyz\right)\ge0\)
\(\Leftrightarrow\left(x+y+z\right)^2\ge0\)
Đây là BĐT luôn đúng nên ta có đpcm.
ミ★ᗪเệų ℌųуềй (ßăйǥ ßăйǥ ²к⁶)★彡 Giải ghê quá, t chẳng hiểu gì.
Đặt \(\left(a;b;c\right)=\left(\frac{x}{y};\frac{y}{z};\frac{z}{x}\right)\)
BĐT \(\Leftrightarrow \sum\limits_{cyc} \frac{xy}{(x+y)^2} \leq \frac{1}{4}+\frac{4xyz}{(x+y)(y+z)(z+x)}\)
Ta có: \(VP-VT=\frac{4\left(x-y\right)^2\left(y-z\right)^2\left(z-x\right)^2}{4\left(x+y\right)^2\left(y+z\right)^2\left(z+x\right)^2}\ge0\)
BĐT hiển nhiên đúng.
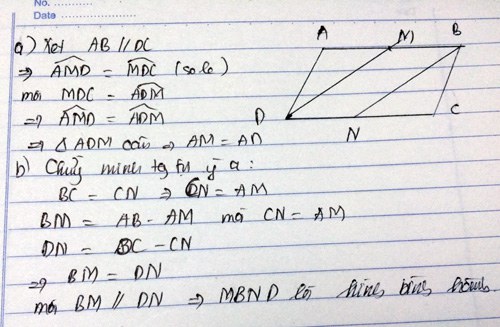
tick hộ rồi giải cho
các bạn tick tôi cho được vào top 100 cái nha bạn nào tick sẽ có nhiều may mắn đến năm mới