Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y=\dfrac{x+z}{2}\)
\(\left(y-4\right)^2=xz\)
\(\left(y-4\right)=\dfrac{x+z-9}{2}\)
3 pt 3 ẩn, kiên trì chút chắc giải được á :D

Lời giải:
Ta có:
$y=xq$
$z=yq=xq^2$
Và:
$2y=x+d$
$3z=2y+d=x+2d$
$\Rightarrow 2xq=x+d$ và $3xq^2=x+2d$
$\Rightarrow 3xq^2-2xq=d$
$\Leftrightarrow xq(3q-2)=d$
Khi đó, thay vô $2xq=x+d$ thì:
$\frac{2d}{3q-2}=\frac{d}{q(3q-2)}+d$
$\Leftrightarrow \frac{2}{3q-2}=\frac{1}{q(3q-2)}+1$ (do $d\neq 0$)
$\Leftrightarrow 2q=1+q(3q-2)$
$\Leftrightarrow 3q^2-4q+1=0$
$\Leftrightarrow (q-1)(3q-1)=0$
Vì $q\neq 1$ nên $q=\frac{1}{3}$

Do 3 số lập thành 1 CSC nên: \(2\left(a+8\right)=1+b\Rightarrow b=2a+15\)
Do 3 số lập thành 1 CSN nên:
\(a^2=b.1\Leftrightarrow a^2=2a+15\)
\(\Leftrightarrow a^2-2a-15=0\Rightarrow\left[{}\begin{matrix}a=5\\b=-3< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow b=2a+15=25\)

Bạn xem lại đề, với a;b;c dương thì biểu thức P không tồn tại max nếu đề hoàn toàn đúng
Muốn P tồn tại max thì a;b;c cần không âm (nghĩa là có thể bằng 0)

Chọn D
Theo tính chất cấp số nhân, Ta có: ac=2/3 b2. Theo hệ thức lượng trong tam giác vuông, Ta có: b=a.sinB, c=a.cosB. vậy Ta có
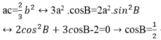
![]()

Ba số \(\frac{2}{{b - a}},\frac{1}{b},\frac{2}{{b - c}}\) theo thứ tự lập thành cấp số cộng nên ta có:
\(\begin{array}{l}\frac{2}{{b - a}} + \frac{2}{{b - c}} = 2.\frac{1}{b} \Leftrightarrow \frac{1}{{b - a}} + \frac{1}{{b - c}} = \frac{1}{b} \Leftrightarrow \frac{{\left( {b - c} \right) + \left( {b - a} \right)}}{{\left( {b - a} \right)\left( {b - c} \right)}} = \frac{1}{b}\\ \Leftrightarrow \frac{{b - c + b - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow \frac{{2b - c - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow b\left( {2b - c - {\rm{a}}} \right) = {b^2} - ab - bc + ac\\ \Leftrightarrow 2{b^2} - bc - {\rm{ab}} = {b^2} - ab - bc + ac \Leftrightarrow {b^2} = {\rm{a}}c\end{array}\).
Vậy ba số \(a,b,c\) theo thứ tự lập thành cấp số nhân.

Theo giả thiết ta có : \(\cot A+\cot C=2\cot B\)
\(\Leftrightarrow\frac{\sin\left(A+C\right)}{\sin A\sin C}=\frac{2\cos B}{\sin B}\)
\(\Leftrightarrow\sin^2B=2\sin B\sin C\cos B=\left[\cos\left(A-C\right)-\cos\left(A+C\right)\right]\cos B\)
\(\Leftrightarrow\sin^2B=\cos\left(A-C\right)\cos B-\cos\left(A+C\right)\cos B=-\cos\left(A-C\right)\cos\left(A+C\right)+\cos^2B\)
\(\Leftrightarrow\sin^2B=-\frac{1}{2}\left(\cos2A+\cos2C\right)+1-\sin^2B=-\frac{1}{2}\left(1-2\sin^2A+1-2\sin^2C\right)+1-\sin^2B\)
\(\Rightarrow2\sin^2B=\sin^2A+\sin^2C\Leftrightarrow2b^2=a^2+c^2\)
Vậy chứng tỏ \(a^2,b^2,c^2\) theo thứ tự đó cũng lập thành một cấp số cộng
Lời giải:
Có:
$b=a+d$
$c=a+2d$
$c=bq$
$a=bq^2$
$\Rightarrow abc=bq^2.b.bq=(bq)^3=8$
$\Rightarrow bq=2$
$\Rightarrow c=2$
$a=bq^2=bq.q=2q$
$b=a+d=2q+d$
$2=c=a+2d=2q+2d\Rightarrow q+d=1$
$\Rightarrow b=2q+d=q+(q+d)=q+1$. Mà $bq=2$ nên:
$q(q+1)=2$
$\Leftrightarrow (q-1)(q+2)=0$
$\Rightarrow q=1$ hoặc $q=-2$
Vì $a,b,c$ đều dương nên $q>0$. Do đó $q=1$