Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

sử dụng bơ du thay x = 3 vào đa thức f(x) ta thấy đa thức f(x) không chia hết cho x - 3 nha

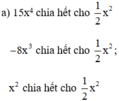
Do đó A = 15x4 - 8x3 + x2 chia hết cho 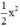 hay A chia hết cho B.
hay A chia hết cho B.
b) A = x2 - 2x + 1 = (x – 1)2
Vậy A chia hết cho x – 1 hay A chia hết cho B.

a) \(x^3-9x^2+6x+16\)
\(\Leftrightarrow x^3+x^2-10x^2+10x-4x-4+20\)
\(\Leftrightarrow x^2\left(x+1\right)-10x\left(x+1\right)-4\left(x+1\right)+20\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-10x-4+20\right)\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-10x+16\right)\)
Vì (x+1) chia hết cho x+1 => \(\left(x+1\right)\left(x^2-10x+16\right)\) chia hết cho x+1
Câu b) Tương tự
Chúc học tốt !!

b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)

\(a,f\left(x\right):g\left(x\right)=\left(3x^4+9x^3+7x+2\right):\left(x+3\right)\\ =\left[3x^3\left(x+3\right)+7\left(x+3\right)-19\right]:\left(x+3\right)\\ =\left[\left(3x^3+7\right)\left(x+3\right)-19\right]:\left(x+3\right)\\ =3x^3+7.dư.19\)
\(c,\) Để \(k\left(x\right)⋮g\left(x\right)\Leftrightarrow-x^3-5x+2m=\left(x+3\right)\cdot a\left(x\right)\)
Thay \(x=-3\)
\(\Leftrightarrow-\left(-3\right)^3-5\left(-3\right)+2m=0\\ \Leftrightarrow27+15+2m=0\\ \Leftrightarrow2m=-42\\ \Leftrightarrow m=-21\)

d: Ta có: f(x):g(x)
\(=\dfrac{x^3-2x^2+3x+5}{x+1}\)
\(=\dfrac{x^3+x^2-3x^2-3x+6x+6-1}{x+1}\)
\(=x^2-3x+6+\dfrac{-1}{x+1}\)
Để f(x) chia hết cho g(x) thì \(x+1\in\left\{1;-1\right\}\)
hay \(x\in\left\{0;-2\right\}\)

b: Ta có: f(x):g(x)
\(=\dfrac{x^3-2x^2+3x+a}{x+1}\)
\(=\dfrac{x^3+x^2-3x^2-3x+6x+6+a-6}{x+1}\)
\(=x^2-3x+6+\dfrac{a-6}{x+1}\)
Để f(x):g(x) là phép chia hết thì a-6=0
hay a=6

a: Thay a=3 vào f(x), ta được:
\(f\left(x\right)=x^3-2x^2+3x+3\)
\(\dfrac{f\left(x\right)}{g\left(x\right)}=\dfrac{x^3-2x^2+3x+3}{x+1}\)
\(=\dfrac{x^3+x^2-3x^2-3x+6x+6-3}{x+1}\)
\(=x^2-3x+6-\dfrac{3}{x+1}\)