Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(=\left(3-x\right)\left(x+1\right)\)
b: \(=3x\left(x-y\right)-5\left(x-y\right)\)
=(x-y)(3x-5)
c: \(=x\left(x-y\right)-10\left(x-y\right)\)
\(=\left(x-y\right)\left(x-10\right)\)
a) \(=x\left(3-x\right)+\left(3-x\right)=\left(3-x\right)\left(x+3\right)\)
b) \(=3x\left(x-y\right)-5\left(x-y\right)=\left(x-y\right)\left(3x-5\right)\)
c) \(=x\left(x-y\right)-10\left(x-y\right)=\left(x-y\right)\left(x-10\right)\)
d) \(=\left(x+y\right)^2-16=\left(x+y-4\right)\left(x+y+4\right)\)
e) \(=\left(x-y\right)\left(x+y\right)-4\left(x+y\right)=\left(x+y\right)\left(x-y-4\right)\)
f) \(=9-\left(4x^2-4xy+y^2\right)=9-\left(2x-y\right)^2=\left(3-2x+y\right)\left(3+2x-y\right)\)
g) \(=y\left(y^2-2xy+x^2-y\right)\)
h) \(=x^2\left(x-3\right)-4\left(x-3\right)=\left(x-3\right)\left(x^2-4\right)=\left(x-3\right)\left(x-2\right)\left(x+2\right)\)
i) \(=x\left(x-y\right)+\left(x-y\right)\left(x+y\right)=\left(x-y\right)\left(2x+y\right)\)

Bạn nên viết đề cho rõ ràng để mọi người hiểu đề và hỗ trợ bạn tốt hơn. Viết đề díu dít vào nhau và không gõ công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) khiến bài của bạn có khả năng bị bỏ qua cao hơn nhé.

a) \(2x\left(x^2-7x-3\right)=2x.x^2-2x.7x-2x.3=2x^3-14x^2-6x\)
b) \(\left(-2x^3+y^2-7xy\right)4xy^2=\left(-2x^3\right)4xy^2+y^24xy^2-7xy.4xy^2=-8x^4y^2+4xy^4-28x^2y^3\)
c) \(\left(-5x^3\right)\left(2x^2+3x-5\right)=-5x^32x^2-5x^33x-5x^3.-5=-10x^5-15x^4+25x^3\)
d) \(\left(2x^2-xy+y^2\right)\left(-3x^3\right)=-3x^32x^2-3x^3.-xy-3x^3y^2=-6x^5+3x^4y-3x^3y^2\)
e) \(\left(x^2-2x+3\right)\left(x-4\right)=x\left(x^2-2x+3\right)-4\left(x^2-2x+3\right)=x^3-2x^2+3x-4x^2+8x-12=x^3-6x^2+11x-12\)
f) \(\left(2x^3-3x-1\right)\left(5x+2\right)=5x\left(2x^3-3x-1\right)+2\left(2x^3-3x-1\right)=10x^4-15x^2-5x+4x^3-6x-2=10x^4+4x^3-15x^2-11x-2\)

a) 2x.(x2 - 7x - 3)
= 2xx2 + 2x(-7x) + 2x(-3)
= 2x2x - 2.7xx - 2.3x
= 2x3 - 14x2 - 6x

e: \(x^2+6x+9-y^2\)
\(=\left(x+3\right)^2-y^2\)
\(=\left(x+3-y\right)\left(x+3+y\right)\)
f: \(x^2-2x+7x-14\)
\(=x\left(x-2\right)+7\left(x-2\right)\)
=(x-2)(x+7)
h: \(5x^2-10xy+5y^2-20\)
\(=5\left(x^2-2xy+y^2-4\right)\)
\(=5\left(x-y-2\right)\left(x-y+2\right)\)

a: \(3x^4-6x^3+2x^2=x^2\left(3x^2-6x+2\right)\)
b: \(x^3y+12x^2y+36xy=xy\left(x^2+12x+36\right)=xy\left(x+6\right)^2\)
c: \(x^3y-9xy^3=xy\left(x^2-9y^2\right)=xy\left(x-3y\right)\left(x+3y\right)\)
d: \(x^2y^2-2xy^2+y^2=y^2\left(x-1\right)^2\)

a, \(x^2-4x+3=0\Leftrightarrow\left(x-3\right)\left(x-1\right)=0\)
TH1 : x = 3 ; TH2 : x = 1
b, \(2x^2-3x-2=0\Leftrightarrow\left(x-2\right)\left(x+\frac{1}{2}\right)=0\)
TH1 : x = 2 ; TH2 : x = -1/2
c, Đặt \(x^2=t\left(t\ge0\right)\)
\(t^2+2t-8=0\Leftrightarrow\left(t-2\right)\left(t+4\right)=0\)
TH1 : t = 2 ; TH2 : t = -4
Tương tự ...
1a)
x2 - 4x + 3 = x2 - x - 3x + 3
= x( x - 1 ) - 3( x - 1 )
= ( x - 1 )( x - 3 )
2c)
2x2 - 3x - 2 = 2x2 + x - 4x - 2
= x( 2x +1 ) - 2( 2x + 1 )
= ( 2x + 1 )( x - 2 )
3e)
x4 + 2x2 - 8 (*)
Đặt t = x2
(*) <=> t2 + 2t - 8
= t2 - 2t + 4t - 8
= t( t - 2 ) + 4( t - 2 )
= ( t - 2 )( t + 4 )
= ( x2 - 2 )( x2 + 4 )
4b) x2 + 4x - 12 = x2 - 2x + 6x - 12
= x( x - 2 ) + 6( x - 2 )
= ( x - 2 )( x + 6 )
d) 2x3 + x - 2x2 - 1 = 2x2( x - 1 ) + 1( x - 1 )
= ( x - 1 )( 2x2 + 1 )
f) x2 - 2xy - 3y2 = ( x2 - 2xy + y2 ) - 4y2
= ( x - y )2 - ( 2y )2
= ( x - y - 2y )( x - y + 2y )
= ( x - 3y )( x + y )

*Tìm giá trị nhỏ nhất
a) \(A=x^2-4x+1\)
Ta có: \(A=x^2-4x+1\)
\(=x^2-4x+4-5=\left(x-2\right)^2-5\)
Ta có: \(\left(x-2\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-2\right)^2-5\ge-5\forall x\)
Dấu '=' xảy ra khi \(\left(x-2\right)^2=0\Leftrightarrow x-2=0\Leftrightarrow x=2\)
Vậy: Giá trị nhỏ nhất của biểu thức \(A=x^2-4x+1\) là -5 khi x=2
b) \(B=4x^2+4x+11\)
Ta có: \(B=4x^2+4x+11\)
\(=\left(2x\right)^2+2\cdot2x\cdot1+1+10=\left(2x+1\right)^2+10\)
Ta có: \(\left(2x+1\right)^2\ge0\forall x\)
\(\Rightarrow\left(2x+1\right)^2+10\ge10\forall x\)
Dấu '=' xảy ra khi \(\left(2x+1\right)^2=0\Leftrightarrow2x+1=0\Leftrightarrow2x=-1\Leftrightarrow x=\frac{-1}{2}\)
Vậy: Giá trị nhỏ nhất của biểu thức \(B=4x^2+4x+11\) là 10 khi \(x=\frac{-1}{2}\)
*Tìm giá trị lớn nhất
e) \(E=5-8x-x^2\)
Ta có: \(E=5-8x-x^2\)
\(=-\left(-5+8x+x^2\right)=-\left(x^2+8x-5\right)=-\left(x^2+8x+16-21\right)=-\left(x+4\right)^2+21\)
Ta có: \(\left(x+4\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x+4\right)^2\le0\forall x\)
\(\Rightarrow-\left(x+4\right)^2+21\le21\forall x\)
Dấu '=' xảy ra khi \(\left(x+4\right)^2=0\Leftrightarrow x+4=0\Leftrightarrow x=-4\)
Vậy: Giá trị lớn nhất của biểu thức \(E=5-8x-x^2\) là 21 khi x=-4
f) \(F=4x-x^2+1\)
Ta có: \(F=4x-x^2+1\)
\(=-\left(-4x+x^2-1\right)\)
\(=-\left(x^2-4x-1\right)=-\left(x^2-4x+4-5\right)\)
\(=-\left(x-2\right)^2+5\)
Ta có: \(\left(x-2\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x-2\right)^2\le0\forall x\)
\(\Rightarrow-\left(x-2\right)^2+5\le5\forall x\)
Dấu '=' xảy ra khi \(\left(x-2\right)^2=0\Leftrightarrow x-2=0\Leftrightarrow x=2\)
Vậy: Giá trị lớn nhất của biểu thức \(F=4x-x^2+1\) là 5 khi x=2
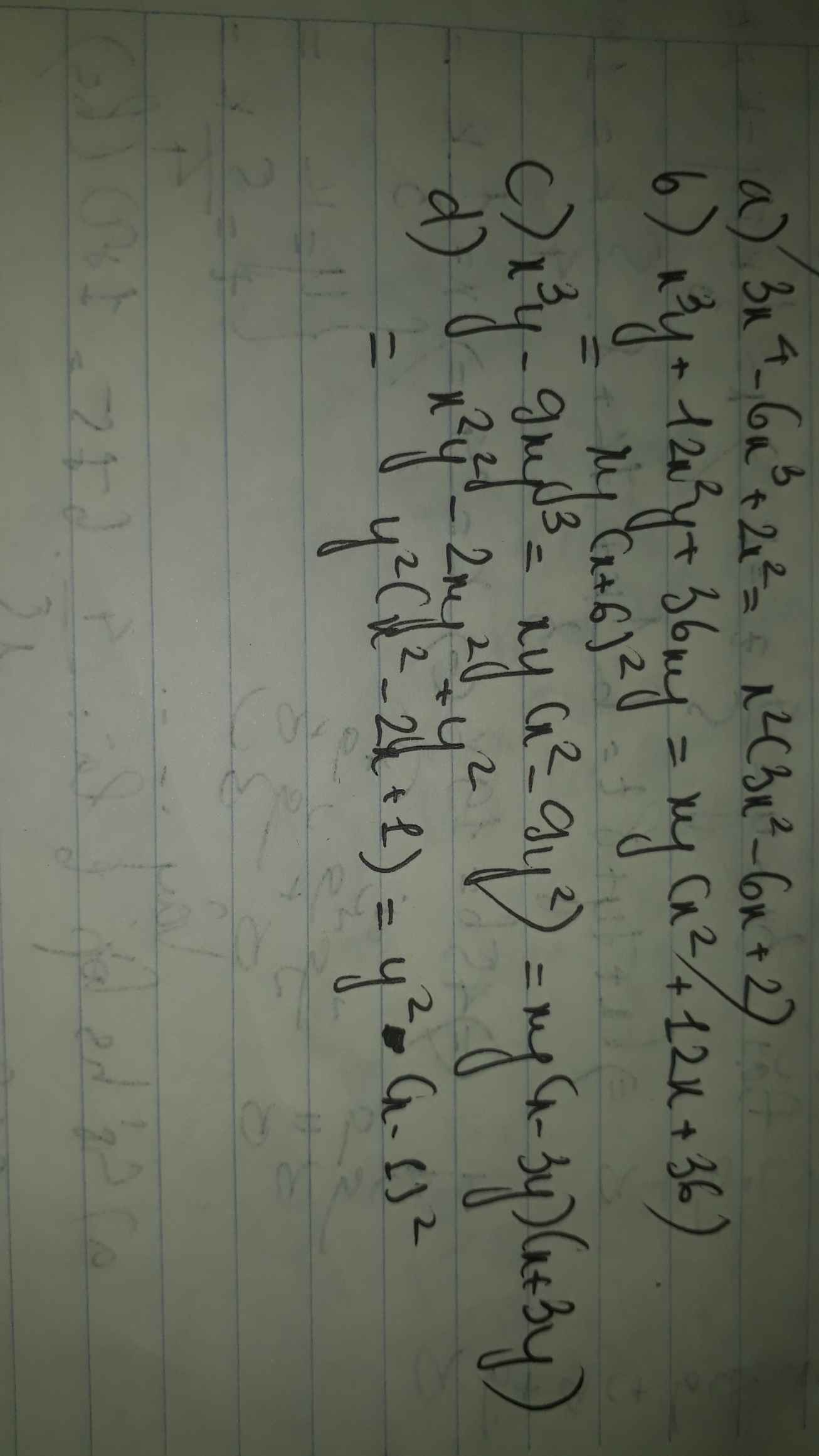
a: A = -2xy + 3/2xy^2 + 1/2xy^2 + xy = -2xy + 2xy^2 + xy = 2xy^2 - xy
b: B = xy^2z + 2xy^2z - xyz - 3xy^2z + xy^2z = 3xy^2z - xyz
c: C = 4x^2y^3 + x^4 - 2x^2 + 6x^4 - x^2y^3 = 7x^4 + 3x^2y^3 - 2x^2
d: D = 3/4xy^2 - 2xy - 1/2xy^2 + 3xy = 5/4xy^2 + xy
e: E = 2x^2 - 3y^3 - z^4 - 4x^2 + 2y^3 + 3z^4 = -2x^2 - y^3 + 2z^4
f: F = 3xy^2z + xy^2z - xyz + 2xy^2z - 3xyz = 6xy^2z - 2xyz
a: A=-2xy+3/2xy^2+1/2xy^2+xy
=-2xy+xy+3/2xy^2+1/2xy^2
=2xy^2-xy
b: \(B=xy^2z+2xy^2z-xyz-3xy^2z+xy^2z\)
\(=xy^2z\left(1+2-3+1\right)-xyz=xy^2z-xyz\)
c: \(=4x^2y^3-x^2y^3+x^4+6x^4-2x^2\)
\(=7x^4-x^2+3x^2y^3\)
d: \(=\dfrac{3}{4}xy^2-\dfrac{1}{2}xy^2+3xy-2xy\)
=1/4xy^2+xy
e: \(=2x^2-4x^2-3y^3+2y^3+3z^4-z^4\)
\(=-2x^2-y^3+2z^4\)
f: \(=xy^2z+3xy^2z+2xy^2z-xyz-3xyz\)
\(=6xy^2z-4xyz\)