Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐKXĐ: \(x\ne1\)
\(\Leftrightarrow\left|2x-1\right|>2\left|x-1\right|\)
\(\Leftrightarrow\left(2x-1\right)^2-\left(2x-2\right)^2>0\)
\(\Leftrightarrow4x-3>0\)
\(\Rightarrow x>\frac{3}{4}\)
\(\Rightarrow x\in\left(\frac{3}{4};1\right)\cup\left(1;+\infty\right)\)
Chẳng đáp án nào đúng cả :)

\(\left(x-a\right)\left(ax+b\right)=0\Rightarrow\left[{}\begin{matrix}x=a\\x=-\frac{b}{a}\end{matrix}\right.\)
\(\Rightarrow\) Nghiệm của BPT: \(\left(-\infty;-\frac{b}{a}\right)\cup\left(a;+\infty\right)\)

Đặt \(f\left(x\right)=\dfrac{x-1}{\left(x-2\right)\left(x-3\right)}.\)
\(x-1=0.\Leftrightarrow x=1.\\ x-2=0.\Leftrightarrow x=2.\\ x-3=0.\Leftrightarrow x=3.\)
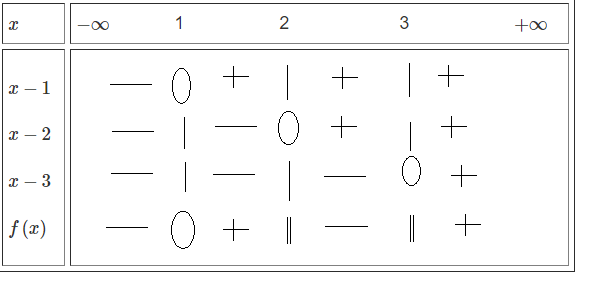
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\) \(\left(1;2\right)\cup\left(3;+\infty\right).\)
\(\Rightarrow B.\)

a/ ĐKXĐ: \(x\ne-1\)
Giả sử x1> x2
\(\Rightarrow f\left(x_1\right)=\frac{x_1}{x_1+1};f\left(x_2\right)=\frac{x_2}{x_2+1}\)
Có \(f\left(x_1\right)-f\left(x_2\right)=\frac{x_1}{x_1+1}-\frac{x_2}{x_2+1}\)
\(=\frac{x_1x_2+x_1-x_1x_2-x_2}{\left(x_1+1\right)\left(x_2+2\right)}=\frac{x_1-x_2}{\left(x_1+1\right)\left(x_2+1\right)}\)
Xét trên khoảng \(\left(-\infty;1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_1+1>0\\x_2+1>0\end{matrix}\right.\Rightarrow\left(x_1+1\right)\left(x_2+1\right)>0\)
Có \(x_1>x_2\Rightarrow x_1-x_2>0\Rightarrow f\left(x_1\right)-f\left(x_2\right)>0\)
=> hàm số đồng biến trên \(\left(-\infty;1\right)\)
làm tương tự trên khoảng \(\left(-1;+\infty\right)\)
b/ \(ĐKXĐ:x\ne2\)
Giả sử x1> x2
\(f\left(x_1\right)-f\left(x_2\right)=\frac{2x_1+3}{2-x_1}-\frac{2x_2+3}{2-x_2}\)
\(=\frac{4x_1-2x_1x_2+6-3x_2-4x_2+2x_1x_2-6+3x_1}{\left(2-x_1\right)\left(2-x_2\right)}\)
\(=\frac{7x_1-7x_2}{\left(2-x_1\right)\left(2-x_2\right)}\)
Xét trên khoảng \(\left(-\infty;2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}2-x_1>0\\2-x_2>0\end{matrix}\right.\Rightarrow\left(2-x_1\right)\left(2-x_2\right)>0\)
Có \(x_1>x_2\Rightarrow7x_1-7x_2>0\)
\(\Rightarrow f\left(x_1\right)-f\left(x_2\right)>0\)
=> hàm số đồng biến trên \(\left(-\infty;2\right)\)
làm tương tự trên \(\left(2;+\infty\right)\)
c/ Có \(-\frac{b}{2a}=-1\)
Mà a=1>0 => hàm số đồng biến trên \(\left(-1;+\infty\right)\) , nghịch biến trên \(\left(-\infty;-1\right)\)
d/ \(-\frac{b}{2a}=1\)
Mà a= -1>0 => hàm số đồng biến trên \(\left(-\infty;1\right)\) , nghịch biến trên \(\left(1;+\infty\right)\)

y xác định khi :
X3 - 1 \(\ne\)0
=> X \(\ne\)1.
Vậy TXD : D =R\ {1} hay D = (-\(\infty\);1) \(\cup\)( 1 ; + \(\infty\))

a/ \(\Leftrightarrow\left[{}\begin{matrix}a>1\\\frac{a+1}{2}< -1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}a>1\\a< -3\end{matrix}\right.\)
b/ \(\left(-\infty;5\right)\cup\left(-3;+\infty\right)=R\) nên với mọi a thì \(\left[a;\frac{a+1}{2}\right]\in\left(-\infty;5\right)\cup\left(-3;+\infty\right)\)
Lời giải:
Ta xét các TH sau:
TH1: \(x\geq 5\)
\(\Rightarrow \left\{\begin{matrix} |2x-4|=2x-4\\ |x+1|=x+1\\ |5-x|=x-5\end{matrix}\right.\Rightarrow |2x-4|+|x+1|-|5-x|=2x+2\)
Để hàm số đc xác định thì \(2x+2\neq 0\Leftrightarrow x\neq -1\), luôn đúng với \(x\geq 5\)
TH2: \(2< x< 5\)
\(\Rightarrow \left\{\begin{matrix} |2x-4|=2x-4\\ |x+1|=x+1\\ |5-x|=5-x\end{matrix}\right.\Rightarrow |2x-4|+|x+1|-|5-x|=4x-8\)
Để hàm số đc xác định thì \(4x-8\neq 0\), điều này luôn đúng với \(2< x< 5\)
TH3: \(-1\leq x\leq 2\)
\(\Rightarrow \left\{\begin{matrix} |2x-4|=4-2x\\ |x+1|=x+1\\ |5-x|=5-x\end{matrix}\right.\Rightarrow |2x-4|+|x+1|-|5-x|=0\)
(Không thỏa mãn)
TH4: \(x< -1\)
\(\Rightarrow \left\{\begin{matrix} |2x-4|=4-2x\\ |x+1|=-(x+1)\\ |5-x|=5-x\end{matrix}\right.\Rightarrow |2x-4|+|x+1|-|5-x|=-2(x+1)\)
Để hàm số đc xác định thì \(-2(x+1)\neq 0\), điều này luôn đúng với mọi \(x< -1\)
Từ các TH trên , ta suy ra \(x\in (2; +\infty)\cup (-\infty; -1)\)
Vậy \(a=-1; b=2\)