Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 8:
$(x-1)(2+x)>0$ thì có 2 TH xảy ra:
TH1: \(\left\{\begin{matrix} x-1>0\\ x+2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x>1\\ x>-2\end{matrix}\right.\Rightarrow x>1\)
TH2: \(\left\{\begin{matrix} x-1< 0\\ x+2< 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x< 1\\ x< -2\end{matrix}\right.\Rightarrow x< -2\)
Vậy $x\in (1;+\infty)$ hoặc $x\in (-\infty; -2)$
Câu 7:
$|x^2+x-12|=|(x-3)(x+4)|$
Nếu $x\geq 3$ thì $(x-3)(x+4)\geq 0$
$\Rightarrow |x^2+x-12|=x^2+x-12$
BPT trở thành: $x^2+x-12< x^2+x+12$ (luôn đúng)
Nếu $3> x> -4(1)$ thì $(x-3)(x+4)< 0$
$\Rightarrow |x^2+x-12|=-(x^2+x-12)$
BPT trở thành: $-(x^2+x-12)< x^2+x+12$
$\Leftrightarrow 2(x^2+x)>0\Leftrightarrow x>0$ hoặc $x< -1$
Kết hợp với $(1)$ suy ra $3>x>0$ hoặc $-1> x> -4$
Nếu $x\leq -4$ thì $(x-3)(x+4)\geq 0$
$\Rightarrow |x^2+x-12|=x^2+x-12$
BPT trở thành: $x^2+x-12< x^2+x+12$ (luôn đúng)
Vậy BPT có nghiệm $x\in (+\infty; 0)$ hoặc $x\in (-\infty; -1)$

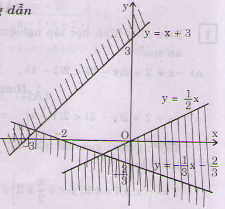
a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
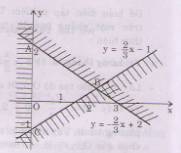
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).

a) Vẽ đường thẳng \(3+2y=0\). Vì điểm O(0;0) có tọa độ thõa mãn bất phương trình nên phần không tô màu là miền nghiệm của bất phương trình:
TenAnh1
TenAnh1
A = (-4.34, -5.96)
A = (-4.34, -5.96)
A = (-4.34, -5.96)
B = (11.02, -5.96)
B = (11.02, -5.96)
B = (11.02, -5.96)
D = (10.28, -5.54)
D = (10.28, -5.54)
D = (10.28, -5.54)
F = (9.98, -5.84)
F = (9.98, -5.84)
F = (9.98, -5.84)
b) Tương tự:
TenAnh1
TenAnh1
A = (-4.34, -5.96)
A = (-4.34, -5.96)
A = (-4.34, -5.96)
B = (11.02, -5.96)
B = (11.02, -5.96)
B = (11.02, -5.96)
D = (10.28, -5.54)
D = (10.28, -5.54)
D = (10.28, -5.54)
F = (9.98, -5.84)
F = (9.98, -5.84)
F = (9.98, -5.84)
H = (10.64, -5.76)
H = (10.64, -5.76)
H = (10.64, -5.76)

a)
<=> f(x) = .
Xét dấu của f(x) ta được tập nghiệm của bất phương trình:
T = ∪ [3; +∞).
b)
<=> f(x) = =
.
f(x) không xác định với x = ± 1.
Xét dấu của f(x) cho tập nghiệm của bất phương trình:
T = (-∞; - 1) ∪ (0; 1) ∪ (1; 3).
c) <=> f(x) =
= .
Tập nghiệm: \(\left(-12;-4\right)\cup\left(-3;0\right)\).

Bài 1:
a) \(\Delta=(1-\sqrt{3})^2-4(\sqrt{3}-2)=12-6\sqrt{3}>0\) nên pt có nghiệm.
Mệnh đề A sai.
b)
\(x^2-x+\frac{1}{4}=(x-\frac{1}{2})^2\geq 0, \forall x\in\mathbb{R}\)
\(\Rightarrow x^2\geq x-\frac{1}{4} , \forall x\in\mathbb{R}\). Mệnh đề B đúng.
c) Sai, $2017$ chỉ có ước là 1 và chính nó nên là số nguyên tố.
d) \(x^2+y^2-\frac{3}{2}y+\frac{3}{4}-xy=(x^2+\frac{y^2}{4}-xy)+\frac{3}{4}y^2-\frac{3}{2}y+\frac{3}{4}\)
\(=(x-\frac{y}{2})^2+\frac{3}{4}(y^2-2y+1)=(x-\frac{y}{2})^2+\frac{3}{4}(y-1)^2\)
\(\geq 0+\frac{3}{4}.0=0\) với mọi $x,y$
\(\Rightarrow x^2+y^2-\frac{3}{2}y+\frac{3}{4}\geq xy\)
Mệnh đề đúng.

Ta có: điều kiện xác định của bpt \(x+3-\dfrac{1}{x+7}< -\dfrac{1}{x+7}\) là \(x\ne-7\)
\(\Rightarrow x=-7\) không phải là nghiệm của bpt trên
Lại có: \(x+3< 2\\ \Leftrightarrow x< 2-3\\ \Leftrightarrow x< -1\)
\(\Rightarrow x=-7\) thỏa mãn bpt \(x+3< 2\) \(\left(-7< -1\right)\)

a) \(\left\{{}\begin{matrix}2x-1\le0\\-3x+5< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\x>\dfrac{5}{3}\end{matrix}\right.\)\(\Leftrightarrow x\in\varnothing\).
b) Vẽ hai đường thẳng \(y=3;2x-3y+1=0\).
Vì điểm \(O\left(0;0\right)\) có tọa độ thỏa mãn bất phương trình \(2x-3y+1>0\) và không thỏa mãn bất phương trình \(3-y< 0\) nên phần không tô màu là miền nghiệm của hệ bất phương trình: \(\left\{{}\begin{matrix}3-y< 0\\2x-3y+1>0\end{matrix}\right.\).
TenAnh1
TenAnh1
A = (-4.34, -5.96)
A = (-4.34, -5.96)
A = (-4.34, -5.96)
B = (11.02, -5.96)
B = (11.02, -5.96)
B = (11.02, -5.96)
\(3x^2+10x+3< 0\)
\(\Rightarrow-3< x< -\frac{1}{3}\)
Đáp án C đúng