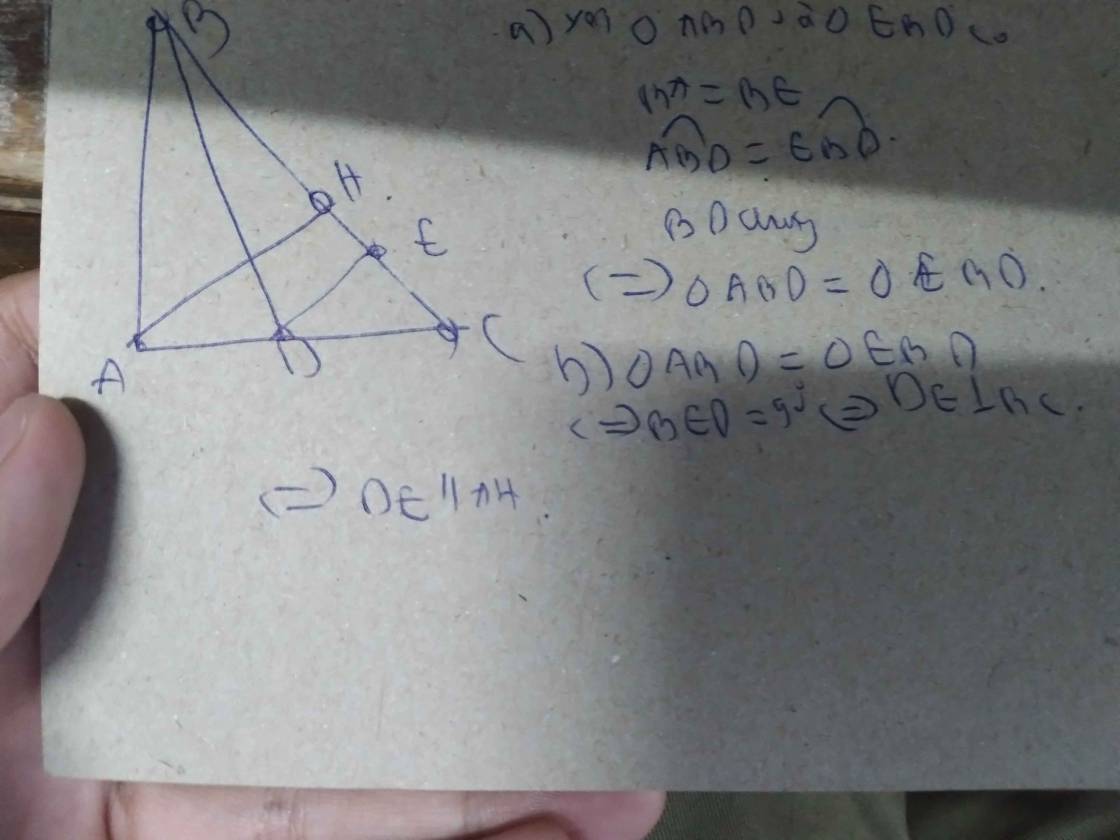Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác BDA và tam giác BDE có:
cạnh BD chung(gt)
góc ABD=gócEBD(BD là tia phân giác góc B)
BA=BE(gt)
=>tam giác ABD=tam giác EBD(c.g.c)=>Đpcm
b) Theo a có tam giác ABD=tam giác EBD=>góc A= góc BED(2 góc tương ứng) =>góc A= góc BED(2 góc tương ứng)
Mà góc A=90 độ=>góc BED=90 độ=>Đpcm
c) Vì tam giác ABC vuông tại A(gt) =>góc B+góc C=90 độ (1)
Vì AH vuông góc với BC(gt) =>góc AHB =90 độ=>tam giác ABH vuông tại H=>góc B+góc BAH=90độ (2)
Từ (1) và (2) =>góc ACH= góc BAH=>Đpcm
Vì góc DEB=90 độ=>DE vuông góc với BC (*)
Mà AH vuông góc với BC (**)
Từ (*) và(**)=>DE // AH(quan hệ vuông góc-song song)=>Đpcm
d) Gọi H là giao của BD và AE
Xét tam giác BAH và tam giác BEH có
cạnh BH chung(gt)
góc ABH- góc EBH(gt)
BA=BE(gt)
=>tam giác ABH=tam giác EBH(c.g.c)
=>HA=HE(2 cạnh tương ứng) (4)
góc BHA=góc BHE
Mà góc BHE+góc BHE=180 độ(2 góc kề bù) => góc BHE=góc BHA=90 độ (3)
+ Từ (3) và(4)=> BD là đường trung trực của AE=>Đpcm

a) Xét tam giác ABD và tam giác EBD có :
AB= BE ( giả thiết ) (1)
Góc B1 = góc B2 ( vì tia BD là tia phân giác ) (2)
BD : cạnh chung (3)
Từ (1) ;(2) và (3) => tam giác ABD = tam giác EBD ( cạnh - góc - cạnh )
b) Vì tam giác ABD = tam giác EBD ( chứng minh ở câu a)
=> góc BAD = góc BED ( cặp góc tương ứng )
Mà góc BAD = 90 độ
=> BED = 90 độ
c) Vì góc BED = 90 độ
=> tam giác BED vuông
d) Vì AH vuông góc với BC ( giả thiết) (1)
và DE vuông góc với BC ( giả thiết ) (2)
Từ (1) và (2) => AH // DE ( điều phải chứng minh).

a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
=>DA=DE và góc BED=góc BAD=90 độ
b; AH vuông góc BC
DE vuông góc BC
=>AH//DE

a, xét tam giác ABD và tam giác EBD có : BD chung
góc ABD = góc EBD do BD là pg của góc ABC (Gt)
BE = BA (gt)
=> tam giác ABD = tam giác EBD (c-g-c)
b, tam giác ABD = tam giác EBD (câu a)
=> DA = DE (đn)
và góc DAB = góc DEB (đn)
góc DAB = 90
=> góc DEB = 90
=> DE _|_ BC
=> tam giác DEC vuông tại E (đn)
=> góc CDE + góc BCA = 90 (đl)
tam giác ABC vuông tại A (gt) => góc ABC + góc BCA = 90 (Đl)
=> góc ABC = góc CDE
c, AH _|_ BC (Gt)
DE _|_ BC (câu b)
=> AH // DE (đl)
B H E A D C
Mình vẽ hơi xấu mong bạn thông cảm:)
a) \(\Delta ABD\) và \(\Delta EBD\) có :
\(BE=BA\)
\(\widehat{ABD}=\widehat{EBD}\) ( vì BD là phân giác )
\(BC:\) cạnh chung
\(\Rightarrow\Delta ABD=\Delta EBD\left(c.g.c\right)\left(1\right)\)
b) Từ ( 1 ) => \(DA=DE\) và \(\widehat{BAD}=\widehat{BED}=90^0\)
Mặt khác , ta có : \(\widehat{ABC}=\widehat{BAC}-\widehat{C}=90^0-\widehat{C}\)
\(\widehat{EDC}=\widehat{DEC}-\widehat{C}=90^0-\widehat{C}\)
\(\Rightarrow\widehat{ABC}=\widehat{EDC}\)
c) Ta có : \(AH\perp BC\), \(DE\perp BC\) ( vì \(\widehat{DEC}=90^0\) ) nên AH//DE