Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hình pạn tự vẽ nha!!!
Bài Làm:
Xét \(\Delta ABC\) có \(DE//AC\left(gt\right)\)
\(\Rightarrow\dfrac{AE}{AB}=\dfrac{CD}{CB}\left(1\right)\) ( Theo định lí Ta - lét )
Lại có: \(DF//AB\left(gt\right)\)
\(\Rightarrow\dfrac{AF}{AC}=\dfrac{BD}{CB}\left(2\right)\) ( Theo định lí Ta - lét )
Từ (1) và (2) \(\Rightarrow\) \(\dfrac{AE}{AB}+\dfrac{AF}{AC}=\dfrac{CD}{CB}+\dfrac{BD}{CB}\)
\(\Leftrightarrow\dfrac{AE}{AB}+\dfrac{AF}{AC}=\dfrac{CD+DB}{CB}=\dfrac{CB}{CB}=1\)
Chúc pạn hok tốt!!!
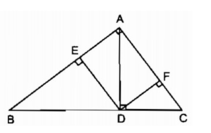
DE và CA cùng vuông góc với AB, do đó
DE // AC.
Theo định lí Ta-lét, ta có:
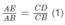
Tương tự, ta có: DF // AB, do đó:
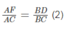
Cộng các vế tương ứng của (1) và (2), ta có:
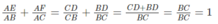
Tổng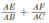 
không thay đổi vì luôn có giá trị bằng 1.
Vậy : Khi độ dài cạnh góc vuông AB, AC của tam giác vuông ABC thay đổi thì tổng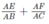 
luôn luôn không thay đổi. Tổng đó luôn có giá trị bằng 1.
