Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
K đối xứng với H qua BC
⇒ BC là trung trực của HK
⇒ BH=BK; CH=CK
Xét ΔBHC và ΔBKC có:
BH=BK (cmt)
CH=CK (cmt)
BC: cạnh chung
Do đó ΔBHC = ΔBKC(c.c.c)
b) Ta có:
ˆBHK = ˆBAH + ˆABH (góc ngoài của ΔABH)
ˆCHK = ˆCAH+ ˆACH (góc ngoài của ΔACH)
⇒ ˆBHC = ˆBHK + ˆCHK
= ˆBAH + ˆABH + ˆCAH + ˆACH
= ˆBAC + ˆABH + ˆACH
Ta lại có:
ˆBAC+ˆABH = 90o (BH⊥AC)
ˆBAC+ˆACH = 90o (CH⊥AB)
⇒2ˆBAC+ˆABH+ˆACH=180o
⇒ˆABH+ ˆACH = 180o− 2ˆBAC
Do đó:
ˆBHC =ˆBAC+ 180o− 2ˆBAC= 180o− ˆBAC= 180o−70o = 110o
Mặt khác:
ˆBHC = ˆBKC (ΔBHC = ΔBKC)
⇒ˆBKC=110

a: Ta có: H và K đối xứng nhau qua BC
nên BC là đường trung trực của HK
Suy ra: BH=BK và CH=CK
Xét ΔBHC và ΔBKC có
BH=BK
BC chung
HC=KC
Do đó: ΔBHC=ΔBKC

a : Gọi O là giao của HK và CB, ta có:
S của tam giác CHB= \(\frac{1}{2}OH\cdot CB\)
S của tam giác BKC=\(\frac{1}{2}KO\cdot CB\)
Mà ta có K là điểm đối xứng với H qua BC => KO=HO
Nên ta có thể thay
S của tam giác BKC=\(\frac{1}{2}OH\cdot CB\)
Hay \(Sbkc=Sbhc\)
Nếu đúng thì cho mk xin **** nha

a,ta có :M đối xứng vs H qua BC
suy ra BC là đường trung trực của đoạn thẳng BC
mà B thuộc đường trung trực của đoạn thẳng BC =>BM=BH
và C thuộc đường trung trực của đoạn thẳng BC =>CM=CH
xét tam giác BMC và tam giác BHC có:BM=BH (chứng minh trên),MC=MH chứng minh trên BC chung
=> tam giác BMC=BHC
b,trọng tâm gica ABC có AM là đường trung trực đồng thời là đường cao của cạnh BC => tam giác ABC cân
=>góc ABC =góc BCA =(180 độ -60 độ ):2=60 độ
mà BM và CM là đường phân giác (tam giác ABC cân)suy ra góc MBC =góc MBC =60 độ :2=30 độ
=>góc BMC=180 độ -30 độ+30 độ=120độ
mà góc BCM=góc BCH =>góc BHC=120độ

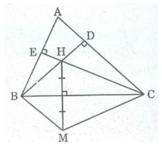
Vì M đối xứng với H qua trục BC
⇒ BC là đường trung trực của HM
⇒ BH = BM (t/chất đường trung trực)
CH = CM (t/chất đường trung trực)
Xét tam giác BHC và tam giác BMC có:
BC chung
BH= BM ( chứng minh trên)
CH = CM (chứng minh trên)
Suy ra: ∆ BHC = ∆ BMC (c.c.c)

Đáp án:
ˆBKC=110oBKC^=110o
Giải thích các bước giải:
a) Ta có:
KK đối xứng với HH qua BCBC
⇒BC⇒BC là trung trực của HKHK
⇒BH=BK;CH=CK⇒BH=BK;CH=CK
Xét ΔBHC∆BHC và ΔBKC∆BKC có:
BH=BK(cmt)BH=BK(cmt)
CH=CK(cmt)CH=CK(cmt)
BC:BC: cạnh chung
Do đó ΔBHC=ΔBKC(c.c.c)∆BHC=∆BKC(c.c.c)
b) Ta có:
ˆBHK=ˆBAH+ˆABHBHK^=BAH^+ABH^ (góc ngoài của ΔABH∆ABH)
ˆCHK=ˆCAH+ˆACHCHK^=CAH^+ACH^ (góc ngoài của ΔACH∆ACH)
⇒ˆBHC=ˆBHK+ˆCHK⇒BHC^=BHK^+CHK^
=ˆBAH+ˆABH+ˆCAH+ˆACH=BAH^+ABH^+CAH^+ACH^
=ˆBAC+ˆABH+ˆACH=BAC^+ABH^+ACH^
Ta lại có:
ˆBAC+ˆABH=90oBAC^+ABH^=90o (BH⊥AC)(BH⊥AC)
ˆBAC+ˆACH=90oBAC^+ACH^=90o (CH⊥AB)(CH⊥AB)
⇒2ˆBAC+ˆABH+ˆACH=180o⇒2BAC^+ABH^+ACH^=180o
⇒ˆABH+ˆACH=180o−2ˆBAC⇒ABH^+ACH^=180o−2BAC^
Do đó:
ˆBHC=ˆBAC+180o−2ˆBAC=180o−ˆBAC=180o−70o=110oBHC^=BAC^+180o−2BAC^=180o−BAC^=180o−70o=110o
Mặt khác:
ˆBHC=ˆBKC(ΔBHC=ΔBKC)BHC^=BKC^(∆BHC=∆BKC)
⇒ˆBKC=110o

a: Xét ΔBHC và ΔBMC có
BH=BM
HC=MC
BC chung
Do đó: ΔBHC=ΔBMC
