Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

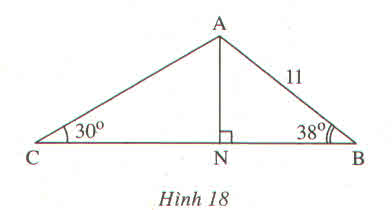
Xét ΔANB vuông tại N có
\(AN=AB\cdot\sin B\)
nên \(AN\simeq6,772\left(cm\right)\)
XétΔACN vuông tại N có
\(AC=\dfrac{AN}{\sin C}=13,544\left(cm\right)\)

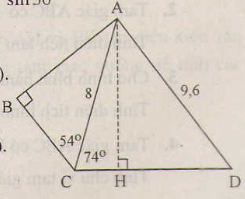
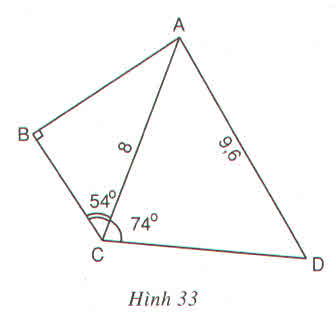
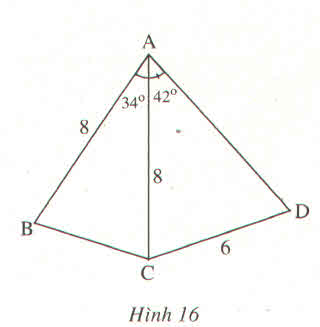
a) Xét tam giác ABC vuông tại B có: AB=AC.sinC=8.sin540≈6,472(cm)AB=AC.sinC=8.sin540≈6,472(cm)
b) Vẽ CD. Xét tam giác ACH có: AH=AC.sinC=8.sin740≈7,690(cm)AH=AC.sinC=8.sin740≈7,690(cm)
Xét tam giác AHD vuông tại H có: sinD=AHAD≈7,6909,6≈0,8010⇒ˆD=530sinD=AHAD≈7,6909,6≈0,8010⇒D^=530
Nhận xét: Để tính được số đo của góc D, ta đã vẽ AH ⊥ CD. Mục đích của việc vẽ đường phụ này là để tạo ra tam giác vuông biết độ dài hai cạnh và có góc D là một góc nhọn của nó. Từ đó tính được một tỉ số lượng giác của góc D rồi suy ra số đo của góc D.

Thay CP = 13,394 vào (1) ta có:
AP = 13,394.cotg 20 ° ≈ 36,801 (cm)
Thay CP = 13,394 vào (2) ta có:
BP = 13,394.cotg 30 ° ≈ 27,526 (cm)

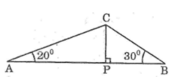
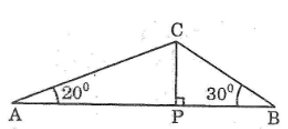
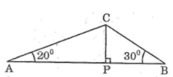
góc ACB=180-20-30=130 độ
Xét ΔABC có
AB/sinC=AC/sinB=BC/sinA
=>BC/sin20=AC/sin30=60/sin130
=>\(BC\simeq26,79\left(cm\right);AC\simeq39,16\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot BC\cdot BA\cdot sinBCA\)
\(=\dfrac{1}{2}\cdot39.16\cdot26.79\cdot sin130=401.83\left(cm^2\right)\)
\(CP=2\cdot\dfrac{S_{ABC}}{AB}=\dfrac{2\cdot401.83}{60}\simeq13,39\left(cm\right)\)
Xét ΔCPA vuông tại P có
tan A=CP/AP
=>13,39/AP=tan20
=>\(AP\simeq36.79\left(cm\right)\)
PB=AB-AP=60-36,79=23,21cm

Tính góc A (= 130 độ ). tam giác ACP vuông tại P => AP = cot A .CP (1)
tam giác BCP vuông tại P => BP = cot B . CP (2)
(1) +(2) => AP + BP =cot A .CP +cot B . CP
<=> AB = CP( cot A + cot B)
<=>60= CP ( cot 130 + cot 20 )
=> CP xấp xỉ 31.4
từ đó có thể dễ dàng tính ra AP và BP

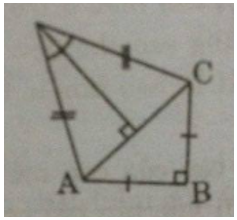
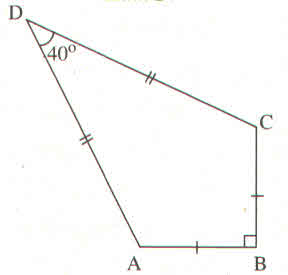
a) Nối AC và kẻ DH⊥ACDH⊥AC
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
AC2=AB2+BC2=122+122=144+144=288AC2=AB2+BC2=122+122=144+144=288
Suy ra: AC=12√2(cm)AC=122(cm)
Ta có: tam giác ACD cân tại D
DH⊥ACDH⊥AC
Suy ra: HA=HC=AC2=6√2(cm)HA=HC=AC2=62(cm)
ˆADH=12ˆADC=20∘ADH^=12ADC^=20∘
Trong tam giác vuông ADH, ta có:
AD=AHsinˆADH=6√2sin20∘≈24,809(cm)AD=AHsinADH^=62sin20∘≈24,809(cm)
b) Ta có:
SABC=12.AB.BC=12.12.12=72SABC=12.AB.BC=12.12.12=72 (cm2)
Trong tam giác vuông ADH, ta có:
DH=AH.cotgˆADH=6√2.cotg20∘≈23,313(cm)DH=AH.cotgADH^=62.cotg20∘≈23,313(cm)
Mặt khác:
SADC=12.DH.AC≈12.23,313.12√2=197,817SADC=12.DH.AC≈12.23,313.122=197,817 (cm2)
Vậy Sdiều =SABC+SADC=72+197,817=269,817=SABC+SADC=72+197,817=269,817 (cm2)
a, nối AC rồi kẻ
Áp dụng định lý Pi-ta-go vào tam giác vuông ABC:
Suy ra:
ta có:tam giác ABC cân tại D
Suy ra:
Trong tam giác vuông ADH, ta có
b, Ta có:
(cm2)
Trong tam giác vuông ADH, ta có:
Mặt khác
(cm2)
Vậy S (cm2)
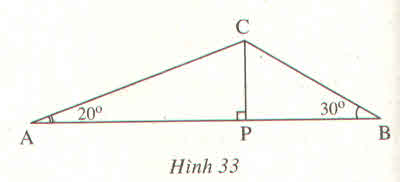


Đặt AP=x suy ra BP=60-x.Ta có phương trình
xtg\(20^0\)=(60-x)tg\(30^0\)
Đ/s:AP ≈36,801cm;BP=23,119cm;CP=13,396cm
Tham khảo nha