Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 4:
a: Xét ΔABM có
AC là đường trung tuyến
AC=MB/2
Do đó: ΔABM vuông tại A
b: Xét ΔMCN và ΔNAP có
MC=NA
\(\widehat{MCN}=\widehat{NAP}\)
CN=AP
Do đó:ΔMCN=ΔNAP
Suy ra: MN=NP
Cm tương tự, ta được: ΔNAP=ΔPBM
Suy ra: NP=PM
hay MN=NP=PM
=>ΔMNP đều

a: Xét ΔABC có
F là trung điểm của AB
E là trung điểm của AC
DO đó: FE là đường trung bình
Suy ra: FE//BC và FE=BC/2(1)
Xét ΔGBC có
I là trung điểm của GB
J là trung điểm của GC
Do đó: IJ là đường trung bình
Suy ra: IJ//BC và IJ=BC/2(2)
Từ (1) và (2) suy ra EF//IJ và EF=IJ
hay EFIJ là hình bình hành
b: Xét ΔAGC có
E là trung điểm của AC
J là trung điểm của GC
Do đó: EJ là đường trung bình
=>EJ//AG
Hình bình hành JIFE trở thành hình chữ nhật khi FE\(\perp\)EJ
=>AG\(\perp\)BC
Xét ΔABC có
AG là đường trung tuyến
AG là đường cao
Do đó: ΔABC cân tại A
hay AB=AC
c: Hình bình hành EFIJ có FJ\(\perp\)EI
nên EFIJ là hình thoi

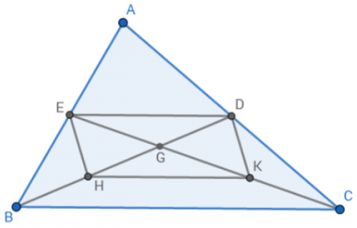
a)
BD là đường trung tuyến của Δ ABC nên D là trung điểm của AC (1)
CE là đường trung tuyến của Δ ABC nên E là trung điểm của AB (2)
Từ (1) và (2) suy ra :
DE là đường trung bình của Δ ABC
=> DE // BC và DE = 1/2 BC
Δ BGC có H là trung điểm của GB và K là trung điểm của GC
suy ra HK là đường trung bình của Δ BGC
=> HK // BC và HK = 1/2 BC
Tứ giác DEHK có DE//BC, HK // BC và DE = HK = 1/2 BC
nên tứ giác
b) DEHK là hình bình hành nên
HG = GD = 1/2 HD và GE = GK = 1/2 EK
Để tứ giác DEHK là hình chữ nhật thì
HD = EK => 1/2 HD = 1/2 EK => GE = GD và GH = GK
GH = GK => 2GH = 2GK => GB = GC
Xét Δ GEB và Δ GDC có
GE = GD Góc EGB = góc DGC GB = GC => ΔGEB = ΔGDC (c.g.c) => BE = CD => 2BE = 2CD => AB = AC => ΔABC cân tại A Vậy đểtứ giác DEHK là hình chữ nhật thì
ΔABC cân tại Ac) BD ⊥ CE => HD ⊥ EK Hình bình hành DEHK có HD ⊥ EK nên DEHK là hình thoi Vậy
nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình thoi

a: Xét ΔABC có
F là trung điểm của AB
E là trung điểm của AC
Do đó: FE là đường trung bình
=>FE//BC và FE=BC/2(1)
Xét ΔGBC có
I là trung điểm của GB
J là trung điểm của GC
Do đó: IJ là đường trung bình
=>IJ//BC và IJ=BC/2(2)
Từ (1) và (2) suy ra EF//JI và EF=JI
=>EFIJ là hình bình hành
c: Khi BE\(\perp\)CF thì FJ\(\perp\)EI
=>EFIJ là hình thoi

