Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình thấy có phân biệt gì giữa hàm đa thức và phân thức đâu bạn.
Theo định nghĩa thì hàm đạt cực trị tại y'=0; đồng biến khi y' > 0 và nghịch biến khi y' < 0.
Cách làm bài hàm bậc 3 ở trên là chưa chính xác.

bạn chỉ cần tách x4-1 thành (x2-1)(x2+1),rồi đặt x2=t là ok

bạn tải về rồi zoom lên ý, vì đây là tớ chụp ảnh nên ảnh nhỏ
mong bạn tải về zoom lên hướng dẫn tớ với

nhờ người ta giải mà cười hihi
em thì bó tay chấm chữ com vào ăn
TXĐ: D=R
\(9^{x^2+x-1}-10.3^{x^2+x-2}+1=0\)
\(\Leftrightarrow9^{x^2+x-1}-10.\frac{3^{x^2+x-1}}{3}+1=0\)
Đặt t = \(3^{x^2+x-1}\) (t>0)
\(\Leftrightarrow t^2-\frac{10}{3}t+1=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}t=3\\t=\frac{1}{3}\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}3^{x^2+x-1}=3\\3^{x^2+x-1}=\frac{1}{3}\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x^2+x-1=1\\x^2+x-1=\frac{1}{3}\end{array}\right.\)

txđ D=R
y'=-3x2+6x+3m
y' là tam thức bậc 2 nên y'=0 có tối đa 2 nghiệm
để hs nb/(0;\(+\infty\) ) thì y' \(\le\) 0 với mọi x \(\in\) (0;\(+\infty\) )
\(\Leftrightarrow\) -3x2 +6x+3m \(\le\) 0 với mọi x \(\in\) (0;\(+\infty\) )
\(\Leftrightarrow\) m\(\le\) x2 -2x với mọi x \(\in\) (0; \(+\infty\) )
xét hs g(x)=x2 -2x
g'(X) =2x-2
g'(x)=0 \(\Leftrightarrow\) x=1
vậy m \(\le\) -1

4.
Đáp án A đúng
\(y'=9x^2+3>0;\forall v\in R\)
6.
Đáp án B đúng
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow\) Hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Do \(\left(2;+\infty\right)\subset\left(1;+\infty\right)\) nên hàm cũng đồng biến trên \(\left(2;+\infty\right)\)
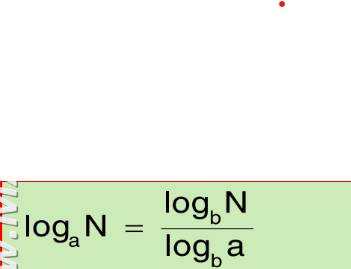











Đây là công thức bạn phải thuộc lòng, còn b là số lớn 0 và khác 1, tùy vào bài tập bạn giải sẽ có số b hợp lý.
ví dụ log12 18= log2 18/log2 12. vậy thì số 2 này từ đâu mà có vậy ạ?