Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử đại lượng y tỉ lệ vs đại lượng x theo hệ số tỉ lệ là k (k ≠ 0 )
⇒ y = xk (1)
Thay x = 4 và y = 12 vào (1) ta có
12 = 4.k
=> k = 3 ( thỏa mãn k khác 0 )
Vậy k = 3
b) Thay k = 3 vào (1) ta có y = 3x
Vậy y = 3x
c) Thay x = - 2 vào công thức y = 3x ta có
y = 3 . ( - 2 )
=> y = - 6
Vậy x = - 2 <=> y = - 6
Thay x = 6 vào công thức y = 3x ta có
y = 6 . 3 = 18
Vậy x = 6 <=> y = 18
## Học tốt
Bài 1:
a) Giả sử đại lượng y tỉ lệ vs đại lượng x theo hệ số tỉ lệ là k (k ≠ 0 )
⇒ y = xk (1)
Thay x = 4 và y = 12 vào (1) ta có
12 = 4.k
=> k = 3 ( thỏa mãn k khác 0 )
Vậy k = 3
b) Thay k = 3 vào (1) ta có y = 3x
Vậy y = 3x
c) Thay x = - 2 vào công thức y = 3x ta có
= 3 . ( - 2 )
=> y = - 6
Vậy x = - 2 <=> y = - 6
Thay x = 6 vào công thức y = 3x ta có
y = 6 . 3 = 18
Vậy x = 6 <=> y = 18
Bài 3:
gọi khối lượng của hai thanh chì là m1 và m2 ( gam )
Do khối lượng và thể tích của vật thể là hai đại lượng tỉ lệ thuận với nhau
⇒ \(\frac{m_1}{12}=\frac{m_2}{17}\)
Áp dụng tính chất của dãy tỉ số bằng nhau , ta có :
\(\frac{m_1}{12}=\frac{m_2}{17}=\frac{m_1+m_2}{12+17}=\frac{56,5}{5}=11,3\)
\(\Rightarrow m_1=135,6\)
\(m_2=192,1\)
Vậy.......................................

Hiệu số phần bằng nhau là:
10 - 8 = 2 phần
Số học sinh khối 6 là:
50 : 2 x 10 = 250 em
Số học sinh khối 7 là:
50 : 2 x 9 = 225 em
Số học sinh khối 8 là:
250 - 50 = 200 em
Đáp số : ...
Gọi số học sinh của 3 khối 6,7,8 lần lượt là: x;y;z ( x;y;z \(\inℕ^∗\)) ( học sinh )
Theo đề bài ta có:
\(\frac{x}{10}=\frac{y}{9}=\frac{z}{8};x-z=50\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{10}=\frac{z}{8}=\frac{y}{9}=\frac{x-z}{10-8}=\frac{50}{2}=25\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{10}=25\Rightarrow x=25.10=250\\\frac{z}{8}=25\Rightarrow z=25.8=200\\\frac{y}{9}=25\Rightarrow y=25.9=225\end{cases}}\)
Vậy số học sinh của khối 6,7,8 lần lượt là: 250 học sinh,225 học sinh và 200 học sinh

a) Gọi số học sinh của bốn khối lần lượt là x , y , z , t ( 0 < x , y, z , t < 600 )
Do số học sinh của bốn khối tỉ lệ với 6 , 7, 8, 9
=> \(\frac{x}{6}=\frac{y}{7}=\frac{z}{8}=\frac{t}{9}\)
Do tổng số học sinh toàn trường là 600 học sinh
=> x + y + z + t = 600
Aps dụng tính chất dãy tỉ số băng nhau , ta có :
\(\frac{x}{6}=\frac{y}{7}=\frac{z}{8}=\frac{t}{9}=\frac{x+y+z+t}{6+7+8+9}=\frac{600}{30}=20\)
=> \(\frac{x}{6}=20\Rightarrow x=20.6=120\)
=> \(\frac{y}{7}=20\Rightarrow y=20.7=140\)
=> \(\frac{z}{8}=20\Rightarrow z=20.8=160\)
=> \(\frac{t}{9}=20\Rightarrow t=20.9=180\)
Vậy bốn khối lần lượt có 120 , 140 , 160 , 180 , học sinh
b)Do số học sinh của bốn khối tỉ lệ với 6 , 7, 8, 9
=> \(\frac{x}{6}=\frac{y}{7}=\frac{z}{8}=\frac{t}{9}\)
Do số học sinh khối 8 ít hơn số học sinh khối 6 là 50 học sinh
=> t - y = 50
Aps dụng tính chất dãy tỉ số bằng nhau ,ta có:
\(\frac{x}{6}=\frac{y}{7}=\frac{z}{8}=\frac{t}{9}=\frac{t-y}{9-7}=\frac{50}{2}=25\)
=> \(\frac{x}{6}=25\Rightarrow x=6.25=150\)
=> \(\frac{y}{7}=25\Rightarrow y=25.7=175\)
=> \(\frac{z}{8}=25\Rightarrow z=8.25=200\)
=> \(\frac{t}{9}=25\Rightarrow t=25.9=225\)
Vậy số học sinh toàn trường là :
150 + 175 + 200 + 225 = 750 ( học sinh )
c)
Do số học sinh của bốn khối tỉ lệ với 6 , 7, 8, 9
=> \(\frac{x}{6}=\frac{y}{7}=\frac{z}{8}=\frac{t}{9}\)
=> \(\frac{y}{7}=20\Rightarrow y=20.7=140\)
Vậy số học sinh khối 6 là 180 học sinh, khối 8 là 140 học sinh
BẠN ĐƯA VỀ BÀITOÀN TLN, R ÁP DỤNG TLT, RỒI BẠN TÍNH =ADTCCDTSBN

Gọi số học sinh của các khối 6,7,8,9 lần lượt là: a,b,c,d
Theo bài ra, ta có: \(\frac{a}{8}=\frac{b}{9}=\frac{c}{7}=\frac{d}{10}\) và a - c = 23
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{a}{8}=\frac{b}{9}=\frac{c}{7}=\frac{d}{10}=\frac{a-c}{8-7}=\frac{23}{1}=23\)
* Số học sinh khối 6 là: 23.8=184 (học sinh)
* Só học sinh khối 7 là: 23.9= 207(học sinh)
* Số học sinh khối 8 là: 23.7= 161(học sinh)
* Số học sinh khối 9 là : 23.10= 230(học sinh)
Vậy số học sinh khối 6,7,8,9 lần lượt là: 184,207,161,230 học sinh
gọi số học sinh 4 khối lần lượt là a,b,c,d
Vì a,b,c,d lần lượt tỉ lệ với 8,9,7,10
\(\Rightarrow\text{ }\frac{a}{8}=\frac{b}{9}=\frac{c}{7}=\frac{d}{10}\)và \(a-c=23\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\frac{a}{8}=\frac{b}{9}=\frac{c}{7}=\frac{d}{10}=\frac{a-c}{8-7}=\frac{23}{2}\)
đề bài sai

Gọi số học sinh các khối 6,7,8,9 lần lượt là x, y, z, t (học sinh)
Số học sinh bốn khối 6 , 7 , 8 , 9 tỉ lệ với các số 9 ; 8 ; 7 ; 6 nghĩa là :
Số học sinh khối 9 ít hơn số học sinh khối 7 là 70 học sinh nghĩa là y – t = 70.
Theo tính chất của dãy tỉ số bằng nhau ta có
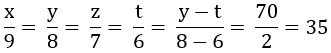
Vậy số học sinh khối 6, 7, 8, 9 lần lượt là 315 ; 280 ; 245 ; 210 học sinh

Lời giải:
Gọi số hs 3 khối 6, 7, 8 lần lượt là $a,b,c$. Theo bài ra ta có:
$\frac{a}{10}=\frac{b}{9}=\frac{c}{8}$ và $a-c=50$
Áp dụng TCDTSBN:
$\frac{a}{10}=\frac{b}{9}=\frac{c}{8}=\frac{a-c}{10-8}=\frac{50}{2}=25$
$\Rightarrow a=25.10=250; b=9.25=225; c=8.25=200$ (học sinh)

Gọi số học sinh của bốn khối 6 , 7, 8, 9 lần lượt là a ;b ; c ; d \(\left(a;b;c;d\inℕ^∗\right)\)
Theo bài ra ta có : \(\frac{a}{9}=\frac{b}{8}=\frac{c}{7}=\frac{d}{6}\); b - d = 70
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a}{9}=\frac{b}{8}=\frac{c}{7}=\frac{d}{6}=\frac{b-d}{8-6}=\frac{70}{2}=35\)
=> a = 35.9 = 315 ;
b = 35 . 8 = 280 ;
c = 35.7 = 245 ;
d = 35.6 = 210
Vậy số học sinh của bốn khối 6 , 7, 8, 9 lần lượt là : 315 học sinh ; 280 học sinh ; 245 học sinh ; 210 học sinh
gọi số học sinh khối 6,7,8,9 lần lượt là a,b,c,d (a,b,c,d thuộc N*; học sinh)
Số học sinh của bốn khối 6 , 7, 8, 9 tỉ lệ với các số 9 , 8 , 7 ,6
=> a/9 = b/8 = c/7 = d/6
=> (b-d)/8-6 = a/9 = b/8 = c/7 = d/6
số học sinh khối 9 ít hơn số hs khối 7 là 70 học sinh => b - d = 70
=> 70/2 = a/9 = b/8 = c/7 = d/6
=> 35 = a/9 = b/8 = c/7 = d/6
=> a = 35.9
b = 35.8
c = 35.7
d = 35.6

Gọi Số học sinh các khối 6, 7, 8, 9 của một trường trung học cơ sở là a, b, c, d
Số học sinh các khối 6, 7, 8, 9 của một trường trung học cơ sở tỉ lệ với 9, 8, 7, 6 tức là a/9 = b/8 = c/7 = d/6
tổng số học sinh của khối 8 và khối 9 ít hơn tổng số học sinh của khối 6 và khối 7 là 120 học sinh tức là a+b-c-d = 120
Áp dụng tỉ lệ thức thôi:
a/9 = b/8 = c/7 = d/6 = (a+b-c-d)/(9+8-7-6) = 120/4 = 30
=> số học sinh khối 6 là a = 270
số học sinh khối 7 là b = 240
số học sinh khối 8 là c = 210
số học sinh khối 9 là d = 180

Gọi số học sinh của từng khối lần luotj là: a, b, c, d (a, b, c, d ∈ N*)
Theo bài ra, ta có: \(\frac{a}{9}=\frac{b}{8}=\frac{c}{7}=\frac{d}{6}\) và a+b+c+d=1050
Theo tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{a}{9}\) \(=\frac{b}{8}=\frac{c}{7}=\frac{d}{6}=\frac{a+b+c+d}{9+8+7+6}=\frac{1050}{30}=35\)
_\(\frac{a}{9}\)= 35 ⇒ 315
_\(\frac{b}{8}\) = 35 ⇒ 280
_ \(\frac{c}{7}\) = 35 ⇒245
_\(\frac{d}{6}\) = 35 ⇒210
Vậy số học sinh của các khối là: khối 6: 315 hs
Khối 7: 280 hs
Koois 8: 245 hs
Khối 9: 210 hs
học tốt
Trả lời:
+ Gọi số học sinh mỗi khối lần lượt là a, b, c, d (học sinh)
Đk: \(a,b,c,d\inℕ^∗\)
+ Vì một trường THCS có 1050 học sinh.
\(\Rightarrow a+b+c+d=1050\)
+ Vì số học sinh của bốn khối 6, 7, 8, 9 lần lượt tỉ lệ với 9, 8, 7, 6
\(\Rightarrow\frac{a}{9}=\frac{b}{8}=\frac{c}{7}=\frac{d}{6}\)
\(\Rightarrow\frac{a}{9}=\frac{b}{8}=\frac{c}{7}=\frac{d}{6}=\frac{a+b+c+d}{9+8+7+6}\)\(=\frac{1050}{30}=35\)(Tính chất dãy tỉ số bằng nhau và a + b + c + d = 1050)
\(\Rightarrow\)\(a=35.9=315\)
\(b=35.8=280\)(Thỏa mãn Đk:\(a,b,c,d\inℕ^∗\))
\(c=35.7=245\)
\(d=35.6=210\)
Vậy số học sinh mỗi khối 6, 7, 8, 9 lần lượt là 315 học sinh, 280 học sinh , 245 học sinh, 210 học sinh.
Hok tốt!
Good girl
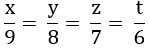
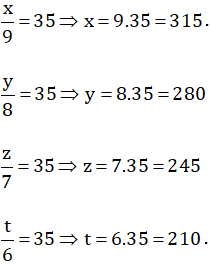
Gọi số học sinh 3 khối lần lượt là x y z ( x,y,z là các số tự nhiên)
Theo bài ra ta có
\(10x=9y=8z\)
và x-60 =z
thay vào và tính nốt là ra
- Kudo-