Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu là: \(C^3_5=455\)
Học sinh bốc được đúng 1 câu hỏi hình và 2 câu đại số có số cách là:
\(C^1_5.C^2_{10}=225\) (cách)
Vậy xác suất cần tìm là: \(P=\frac{225}{455}=\frac{45}{91}\)

http://www.toanhocnhatrang.com/2015/05/bai-toan-so-298.html
Gọi A là tập hợp cách chọn đề có 3 câu dễ, 1 câu khó, 1 câu trung bình.
B là tập hợp cách chọn đề có 2 câu dễ, 2 câu khó, 1 câu trung bình
C là tập hợp cách chọn đề có 2 câu dễ, 1 câu khó, 2 câu trung bình
D là tập hợp cách chọn đề thỏa mãn yêu cầu đề ra. Ta có:
D = A \(\cup\) B \(\cup\) C
ngoài ra A,B,C đôi một không giao nhau. Theo quy tắc cộng ta có
\(\left|D\right|\) = \(\left|A\right|\) + \(\left|B\right|\) + \(\left|C\right|\) (1)
Theo quy tắc nhân ta có
\(\left|A\right|\) = \(C_{15}^3\).\(C_5^1\).\(C_{10}^1\) = 22750
\(\left|B\right|\) = \(C_{15}^2\).\(C_5^2\).\(C_{10}^1\) = 10500
\(\left|C\right|\) = \(C_{15}^2\).\(C_5^1\).\(C_{10}^2\) = 23625
Thay vào (1) ta có \(\left|D\right|\) = 56875
Vậy có 56875 cách chọn đề kiểm tra.

Đáp án A
Lấy ngẫu nhiên từ ngân hàng đề thi 4 câu hỏi để lập một đề thi
có C 20 4 = 4845 đề thi.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 2 câu đã thuộc
có C 10 2 . C 10 2 = 2025 trường hợp.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 3 câu đã thuộc
có C 10 3 . C 10 1 = 1200 trường hợp.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 4 câu đã thuộc
có C 10 4 = 210 trường hợp.
Do đó, thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc
có 2025 + 1200 + 210 = 3435 trường hợp.
Vậy xác suất để thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc là
3435 4845 = 229 323

Đáp án A
Lấy ngẫu nhiên từ ngân hàng đề thi 4 câu hỏi để lập một đề thi có C 20 4 = 4845 đề thi.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 2 câu đã thuộc
có C 10 2 . C 10 2 = 2025 trường hợp.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 3 câu đã thuộc
có C 10 3 . C 10 1 = 1200 trường hợp.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 4 câu đã thuộc
có C 10 4 = 210 trường hợp.
Do đó, thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc
có 2025 + 1200 +210 =3435 trường hợp.
Vậy xác suất để thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc là
3435 4845 = 229 323

Đáp án A
Bạn Nam chọn 3 trong 10 câu nên ![]()
Gọi A là biến cố “Nam chọn ít nhất một câu hình học”.
Khi đó ![]() : “Nam không chọn được câu hình học nào” hay Nam chỉ chọn toàn câu đại số
: “Nam không chọn được câu hình học nào” hay Nam chỉ chọn toàn câu đại số
![]()
![]()
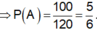

Trong không gian mẫu \(\Omega\) là tập hợp gồm tất cả các cặp hai bộ 3 câu hỏi, mà ở vị trí thứ nhất của cặp là bộ 3 câu hỏi thí sinh A chọn và ở vị trí thứ hai của cặp là bộ 3 câu hỏi thí sinh B chọn
Vì A cũng như B đều có \(C_{10}^3\) cách chọn 3 câu hỏi tứ 10 câu hỏi thí sinh nên theo quy tắc nhân ta có \(n\left(\Omega\right)=\left(C_{10}^3\right)^2\)
Kí hiệu X là biến cố " bộ 3 câu hỏi A chọn và bộ 3 câu hỏi B chọn là giống nhau"
Vì mỗi cách chọn 3 câu hỏi của A, B chỉ có duy nhất cách chọn 3 câu hỏi giống như A nên \(n\left(\Omega_X\right)=C_{10}^3.1=C_{10}^3\)
Vì vậy \(P\left(X\right)=\frac{n\left(\Omega_X\right)}{n\left(\Omega\right)}=\frac{C^3_{10}}{\left(C^3_{10}\right)^2}=\frac{1}{C^3_{10}}=\frac{1}{120}\)

Đáp án A
Ta xét 2 trường hợp
TH1:
Đề thi có 9 câu hỏi nằm trong 25 câu mà học sinh nắm được
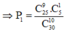
TH2:
Đề thi có 10 câu hỏi nằm trong 25 câu mà học sinh nắm được
![]()
Vậy xác suất cần tính là
![]()

Ít nhất 1 câu hình học, nhiều nhất là 3 câu hình học, bởi giới hạn chỉ được bốc 3 câu hỏi
Khong gian mau: \(n\left(\Omega\right)=C^3_{15}\)
TH1: Bốc 1 câu hình học và 2 câu đại số
\(C^1_5.C^2_{10}\)
TH2: Bốc 2 câu hình học và 1 câu đại số
\(C^2_5.C^1_{10}\)
TH3: Bốc 3 câu hình học
\(C^3_5\)
\(\Rightarrow C^1_5.C^2_{10}+C^2_5.C^1_{10}+C^3_5=..\)
\(p\left(A\right)=\dfrac{C^1_5.C^2_{10}+C^2_5.C^1_{10}+C^3_5}{C^3_{15}}=...\)
Ω: "Chọn 3 câu hỏi từ 15 câu."
⇒ n(Ω) = \(C^3_{15}=455\)
A: "Chọn được ít nhất 1 câu hỏi Hình học."
⇒ \(\overline{A}\): "Không chọn được câu Hình học nào."
\(\Rightarrow n\left(\overline{A}\right)=C^3_{10}=120\)
\(\Rightarrow P\left(\overline{A}\right)=\dfrac{120}{455}=\dfrac{24}{91}\)
\(\Rightarrow P\left(A\right)=1-P\left(\overline{A}\right)=\dfrac{67}{91}\)
Bạn tham khảo nhé!