Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

nếu cậu muốn giá trị tuyệt đối thay vì cái dấu ngoặc vuông ấy thì chỉ cần bấm và giữ shift với phím bên trái của phím end là ra giá trị tuyệt đối thôi

Ta có :
\(K=\frac{2\sqrt{x}+3}{\sqrt{x}-5}=\frac{2\sqrt{x}-10}{\sqrt{x}-5}+\frac{13}{\sqrt{x}-5}=2+\frac{13}{\sqrt{x}-5}\)là số nguyên dương
<=> 13 chia hết cho \(\sqrt{x}-5\)
<=> \(\sqrt{x}-5\inƯ\left(13\right)=\left\{-13;-1;1;13\right\}\)
<=> \(\sqrt{x}\in\left\{-12;4;6;18\right\}\)
<=> \(x\in\left\{16;36;324\right\}\) (vì \(\sqrt{x}\ge0\))
Do x nguyên và x có GTLN nên x = 324

a,Nx: (x+1)2008>=0 với mọi x
=>20- (x+1)2008< hoặc = 20
=> GTLN của A là 20 tại (x+1)2008=0
=> x+1=0
=> x=-1
Vậy GTLN của A là 20
b,Nx: /3-x/> hoặc= 0 với mọi x
=>1010-/3-x/ < hoặc = 0
=>GTLN của B là 1010 tại /3-x/=0
=>3-x=0
=>x=3
c, Nx : (x-1)2 > hoặc = 0
=> (x-1)2 +90 > hoặc = 90
=> GTNN của C là 90 tại (x-1)2=0
=> x-1=0
=> x=1
Vậy GTNN của C là 90
d, Nx: /x+4/> hoặc =0
=> /x+4/ +2015 > hoặc = 2015 với mọi x
=>GTNN của D là 2015 tại /x+4/=0
=> x+4=0
=> x= -4
Vậy GTNN của D là 2015

Chọn đáp án B.
Bằng cách sử dụng điều kiện tồn tại nghiệm của phương trình, chúng ta có: Khi a = 0 thì hàm số chỉ đạt giá trị lớn nhất (khi b < 0) hoặc chỉ đạt giá trị nhỏ nhất (khi b > 0). Còn khi
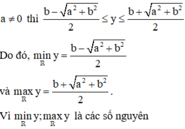
nên tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên khi và chỉ khi
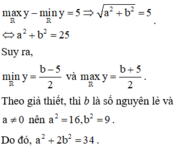

Ta có :
\(\frac{\left|2x-3\right|+2^{2015}}{\left|3-2x\right|+3^{2015}}=\frac{\left|2x-3\right|+2^{2015}}{\left|2x-3\right|+3^{2015}}\) có GTNN
\(\Leftrightarrow\left|2x-3\right|\) có GTNN
\(\Leftrightarrow\left|2x-3\right|=0\)
\(\Leftrightarrow2x=3\)
\(\Leftrightarrow x=1,5\)

Chọn đáp án B
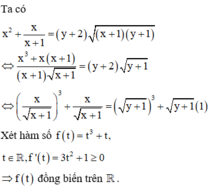
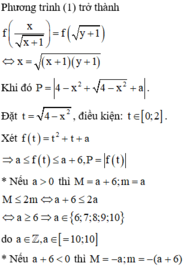
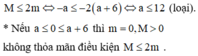
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.

a)ta có A=n-2/n+5(điều kiện như trên)
A=(n+5-7)/n+5
A=1-(7/n+5)
vì 1 là số nguyên nên để A là số nguyên thì 7 phải chia hết cho n+5
nên n+5 thuộc ước của 7
n+5 thuộc -7;-1;1;7
n=-12;-6;-4;2
b)A đạt giá trị nhỏ nhất là-6 khi n= -4(bạn tính ra nhé còn mình thì tính luôn)
B=(-4+5)^2014+2013
B=1^2014+2013
B=2014

Đáp án A
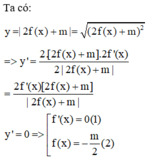
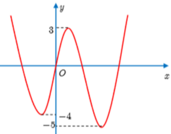
Bài toán cần 5 điểm cực trị => Tổng số nghiệm của (1) và (2) phải là 5
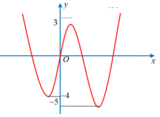
Đối với (1) => số nghiệm chính là số điểm cực trị. Nhìn vào đồ thị => có 3 cực trị
=> Phương trinh (2) phải có 2 nghiệm khác 3 nghiệm trên. Nhìn vào đồ thị ta thấy
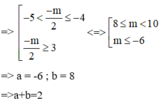

Áp dụng BĐT : \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) ta được:
P=-|3x-18|-|3x+7|=-|18-3x|-|3x+7|=-(|18-3x|+|3x+7|)\(\le\)-25
Dấu "=" xảy ra khi: (18-3x)(3x+7)\(\ge\)0
Giải cái đó ra bạn sẽ được: -7/3 \(\le x\le\)6
Mà x nguyên nên: x={-2;-1;0;1;2;3;4;5;6} có 9 phần tử
Vậy chọn C
Áp dụng \(\left|a\right|-\left|b\right|\le\left|a-b\right|\) (dấu = xảy ra khi a,b > 0), ta có :
\(P=-\left|3x-18\right|-\left|3x+7\right|=-\left|3x-18\right|-\left|7+3x\right|\le-\left|\left(3x-18\right)-\left(7+3x\right)\right|\)
\(=-\left|3x-18-7-3x\right|=-\left|-18-7\right|=-25\)
GTLN của P là -25 <=> 3x - 18 > 0 và 3x + 7 > 0
<=> 3x > 18 và 3x > -7 => x > 6
Vậy có vô số giá trị của x thỏa mãn P có GTLN với điều kiện x > 6 và x là số nguyên