Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Một bạn học sinh làm 2 môn sẽ có 36 cách chọn đề, do đó ![]()
Hai bạn Hùng và Vương có chung một mã đề thi thì cùng mã toán hoặc cùng mã tiếng anh do đó ![]()
Vậy xác suất cần tính là 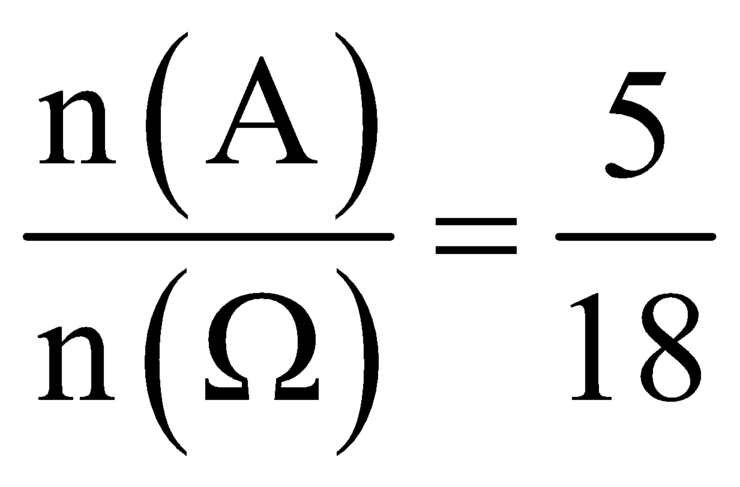

Đáp án A
Kí hiệu học sinh các lớp 12A, 12B,12C lần lượt là A,B,C
Ta sẽ xếp 5 học sinh của lớp 12C trước, khi đó xét các trường hợp sau
Trường hợp1:
CxCxCxCxCx với x thể hiện là ghế trống.
Khi đó, số cách xếp là 5!5! cách.
Trường hợp 2: xCxCxCxCxC giống với TH1
⇒ có 5!5! cách xếp
Trường hợp 3: CxxCxCxCxC với xx là hai ghế trống liền nhau
Chọn 1 học sinh lớp 12A và 1 học sinh lớp 12B vào hai ghế trống đó
⇒ 2.3.2! cách xếp
Ba ghế trống còn lại ta sẽ xếp 3hoc sinh còn lại của 2 lớp 12A-12B
⇒ 3! cách xếp.
Do đó, TH3 có 2.3.2!.3!.5! cách xếp
Ba TH4. CxCxxCxCxC
TH5. CxCxCxxCxC
TH6. CxCxCxCxCxx tương tự
Vậy có tất cả 2.5!5!+4.2.3.2!.3!.5!=63360 cách xếp cho các học sinh
Suy ra xác suất cần tính là
P = 63360 10 ! = 11 630

Đáp án D
Coi 5 bạn của cả 12A và B vào một lớp 12X nào đó
Do số lượng ở đề nên ta có hai trường hợp
TH1. Các bạn 12C và 12X xen kẽ nhau.
Có 5 ! . 5 ! . 2 ! = 28800 cách
TH2. Có hai bạn lớp 12A và 12B dính với nhau
Ta có như 12X chỉ có 4 bạn. rồi lại làm xen kẽ
Chọn 2 bạn dính nhau và hoán vị 2 bạn đó có 12 cách, 5 bạn 12C tạo ra 4 khe để 4 bạn của lớp 12X đứng vào nên có tất cả là
12.5!.4!=34560

Đáp án A
Kí hiệu học sinh các lớp 12A, 12B, 12C lần lượt là A, B, C
Ta sẽ xếp 5 học sinh của lớp 12C trước, khi đó xét các trường hợp sau:
TH1: CxCxCxCxCx với x thể hiện là ghế trống. Khi đó, số cách xếp là ![]() cách.
cách.
TH2: xCxCxCxCxC giống với TH1=> có ![]() cách xếp.
cách xếp.
TH3: CxxCxCxCxC với xx là hai ghế trống liền nhau.
Chọn 1 học sinh lớp 12A và 1 học sinh lớp 12B vào hai ghế trống đó => ![]() cách xếp.
cách xếp.
Ba ghế trống còn lại ta sẽ xếp 3 học sinh còn lại của 2 lớp 12A-12B => ![]() cách xếp.
cách xếp.
Do đó, TH3 có ![]() cách xếp.
cách xếp.
Ba TH4. CxCxxCxCxC.
TH5. CxCxCxxCxC.
TH6. CxCxCxCxCxx tương tự TH3.
Vậy có tất cả ![]() cách xếp cho các học sinh.
cách xếp cho các học sinh.
Suy ra xác suất cần tính là
![]()

Đáp án D
Không gian mẫu là: Ω = 6 4
TH1: Môn Toán trùng mã đề thi môn Tiếng Anh không trùng có:
Bạn Hùng chọn 1 mã toán có 6 cách và 6 cách chọn mã môn Tiếng Anh khi đó Vương có 1 cách là phải giống Hùng mã Toán và 5 cách chọn mã Tiếng Anh có 6.1.6.5 = 180 cách.
TH2: Môn Tiếng Anh trùng mã đề thi môn Toán không trùng có: 6.1.6.5 = 180 cách.
Vậy P = 180 + 180 6 4 = 5 18

Chọn A
Ta đánh số các vị trí từ 1 đến 8.
Số phần tử không gian mẫu là ![]()
Gọi A là biến cố: “xếp được tám bạn thành hàng dọc thỏa mãn các điều kiện: đầu hàng và cuối hàng đều là nam và giữa hai bạn nam gần nhau có ít nhất một bạn nữ, đồng thời bạn Quân và bạn Lan không đứng cạnh nhau”.
TH1: Quân đứng vị trí 1 hoặc 8 => có 2 cách
Chọn một trong 3 bạn nam xếp vào vị trí 8 hoặc 1 còn lại => có 3 cách.
Xếp 2 bạn nam còn lại vào 2 trong 4 vị trí 3,4,5,6 mà 2 nam không đứng cạnh nhau
=> có 6 cách
Xếp vị trí bạn Lan có 3 cách.
Xếp 3 bạn nữ vào 3 vị trí còn lại có 3! cách.
=> TH này có: 2.3.6.3.3! = 648 cách
TH2: Chọn 2 bạn nam ( khác Quân) đứng vào 2 vị trí 1 hoặc 8 có A 3 2 cách.
Xếp Quân và bạn nam còn lại vào 2 trong 4 vị trí 3,4,5,6 mà 2 nam không đứng cạnh nhau => có 6 cách
Xếp vị trí bạn Lan có 2 cách.
Xếp 3 bạn nữ vào 3 vị trí còn lại có 3! cách.
=> TH này có: ![]()
![]()
Vậy xác suất của biến cố A là ![]()

TH1: 5 học sinh lớp C đứng cách nhau đúng 1 vị trí
- Chọn vị trí cho nhóm 5 học sinh lớp C: 2 cách (đứng đầu hàng hoặc ko đứng đầu hàng)
- Hoán vị 5 học sinh lớp C: 5! cách
- Hoán vị 5 học sinh lớp A và B: 5! cách
\(\Rightarrow2.5!.5!\) cách cho TH1
TH2: 5 học sinh lớp C trong đó có 2 bạn đứng cách nhau 2 vị trí
Chọn vị trí cho 2 người kề nhau: 4 cách
Hoán vị 5 học sinh lớp C: 5! cách
Chọn 1 học sinh lớp A, 1 học sinh lớp B xếp vào 2 vị trí liền kề nói trên: \(C_2^1.C_3^1.2!\) cách
Xếp vị trí cho 3 người còn lại: 3! cách
\(\Rightarrow4.5!.C_2^1.C_3^1.2!.3!\) cách cho TH2
Tổng cộng: \(TH1+TH2=...\)

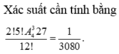
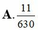

Cái này bạn nhận xét thôi: số cách xếp sao cho ko có bạn nào cùng lớp bằng số cách xếp sao cho ba bạn M2,N2,P2(Với M2,N2,P2 là 3 bạn của lớp A1) ko đứng cạnh nhau trừ đi số cách xếp sao cho ba bạn M2,N2,P2 ko đứng cạnh nhau và hai bạn M1,N1(M1,N1 là hai bạn của lớp A1) đứng cạnh nhau