Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = \(\dfrac{2\left(3\sqrt{x}+2\right)+4}{3\sqrt{x}+2}\)
= \(2+\dfrac{4}{3\sqrt{x}+2}\)
Để A nguyên
<=> \(\dfrac{4}{3\sqrt{x}+2}\) nguyên
<=> \(4⋮3\sqrt{x}+2\)
Ta có bảngg
| \(3\sqrt{x}+2\) | 1 | -1 | 2 | -2 | 4 | -4 |
| x | \(\varnothing\) | \(\varnothing\) | 0 | \(\varnothing\) | \(\dfrac{4}{9}\) | \(\varnothing\) |
| Thử lại | tm | loại |
KL: x = 0
A=\(\dfrac{6\sqrt{x}+8}{3\sqrt{x}+2}\)=\(\dfrac{2(3\sqrt{x}+4)}{3\sqrt{x}+2}\)=\(2\cdot\left(1+\dfrac{2}{3\sqrt{x}+2}\right)\)
Để A∈Z
Thì \(3\sqrt{x}+2\)∈Ư(2)
Tức là \(3\sqrt{x}+2\)∈\(\left\{1;-1;2;-2\right\}\)
\(3\sqrt{x}+2=1\)(vô lí);\(3\sqrt{x}+2=-1\)(vô lí);\(3\sqrt{x}+2=-2\)(vô lí)
\(3\sqrt{x}+2=2\)=>x=0
Vì 0∈Z
Vậy x=0 thì thỏa mãn đề bài

Đề: Dẫn 17,92 lít khí hidro đi qua ống sứ m gam , 1 oxit sắt FexOy nung nóng sau phản ứng thu được 2,4*10^23 phân tử nước và hỗn hợp X gồm 2 chất rắng nặng 28.4 g

\(a,\frac{a+b}{2}\ge\sqrt{ab}\Rightarrow a+b\ge2\sqrt{ab}\)
\(\Rightarrow\left(a+b\right)^2\ge4ab\)
\(\Rightarrow a^2+b^2+2ab\ge4ab\)
\(\Rightarrow a^2-2ab+b^2\ge0\)
\(\Rightarrow\left(a-b\right)^2\ge0\)( luôn đúng )
\(\Rightarrow\frac{a+b}{2}\ge\sqrt{ab}\)

Câu 1:
G/s \(\sqrt{7}\) là số hữu tỉ có thể viết dưới dạng phân số tối giản \(\frac{a}{b}\) \(\left(a,b\inℤ\right)\)
=> \(\frac{a}{b}=\sqrt{7}\)
<=> \(\left(\frac{a}{b}\right)^2=7\)
=> \(a^2=7b^2\)
=> \(a^2⋮b^2\) , mà theo đề bài phân số tối giản
=> a không chia hết cho b => a2 không chia hết cho b2
=> vô lý
=> \(\sqrt{7}\) là số vô tỉ
Câu 2:
a) \(\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(=a^2c^2+2abcd+b^2d^2+a^2d^2-2abcd+b^2c^2\)
\(=\left(a^2c^2+a^2d^2\right)+\left(b^2c^2+b^2d^2\right)\)
\(=a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)\)
\(=\left(a^2+b^2\right)\left(c^2+d^2\right)\)
b) Ta có: \(\left(ac+bd\right)^2=a^2c^2+2abcd+b^2d^2\)
\(=a^2c^2+2\sqrt{a^2d^2.b^2c^2}+b^2d^2\)
\(\le a^2c^2+a^2d^2+b^2c^2+b^2d^2=\left(a^2+b^2\right)\left(c^2+d^2\right)\) ( bất đẳng thức Cauchy )
Dấu "=" xảy ra khi: \(ad=bc\Leftrightarrow\frac{a}{c}=\frac{b}{d}\)

a.
FN là tiếp tuyến tại N \(\Rightarrow\widehat{FNO}=90^0\)
\(\Rightarrow\) 2 điểm P và N cùng nhìn OF dưới 1 góc vuông nên tứ giác ONFP nội tiếp đường tròn đường kính ON
b.
Trong tam giác MQF, do \(PQ\perp ME\) và \(MN\perp FQ\Rightarrow O\) là trực tâm
\(\Rightarrow FO\perp MQ\) tại D
Hai điểm D và N cùng nhìn MF dưới 1 góc vuông
\(\Rightarrow DNFM\) nội tiếp
\(\Rightarrow\widehat{FDN}=\widehat{FMN}\) (cùng chắn FN) (1)
Hai điểm D và P cùng nhìn OM dưới 1 góc vuông
\(\Rightarrow MDOP\) nội tiếp
\(\Rightarrow\widehat{FMN}=\widehat{FDP}\) (cùng chắn OP) (2)
(1);(2) \(\Rightarrow\widehat{FDP}=\widehat{FDN}\)
\(\Rightarrow DF\) là phân giác của \(\widehat{PDN}\)
c.
Do MN là đường kính và E thuộc đường tròn \(\Rightarrow\widehat{MEN}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{MEN}=90^0\Rightarrow NE\perp ME\)
Áp dụng hệ thức lượng trong tam giác vuông MNF với đường cao NE:
\(MN^2=ME.MF\Rightarrow\left(2R\right)^2=ME.MF\)
\(\Rightarrow ME.MF=4R^2\)
Từ đó áp dụng BĐT Cô-si ta có:
\(MF+2ME\ge2\sqrt{MF.2ME}=2\sqrt{8R^2}=4R\sqrt{2}\)
Dấu "=" xảy ra khi \(MF=2ME\Rightarrow E\) là trung điểm MF
\(\Rightarrow NE\) là trung tuyến ứng với cạnh huyền
\(\Rightarrow NE=\dfrac{1}{2}MF=ME\)
\(\Rightarrow E\) là điểm chính giữa cung MN








 giúp vs m đg cần gấp
giúp vs m đg cần gấp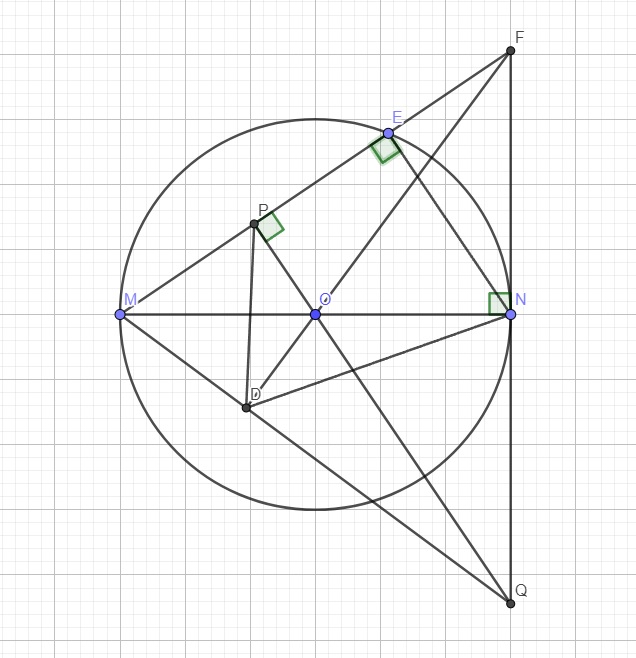
`A=(6sqrtx+8)/(3sqrtx+2)`
`=(6sqrtx+4+4)/(3sqrtx+2)`
`=2+4/(3sqrtx+2)>2AAx>=0(1)`
Vì `3sqrtx>=0`
`=>3sqrtx+2>=2`
`=>4/(3sqrtx+2)<=2`
`=>A<=4(2)`
`(1)(2)=>2<A<=4`
Mà `A in ZZ`
`=>A in {3,4}`
`**A=3`
`<=>4/(3sqrtx+2)=1`
`<=>4=3sqrtx+2`
`<=>3sqrtx=2`
`<=>x=4/9`
`**A=4`
`<=>4/(3sqrtx+2)=2`
`<=>6sqrtx+4=4`
`<=>6sqrtx=0`
`<=>sqrtx=0`
`<=>x=0`
đk: \(x\ge0\)
A = \(\dfrac{2\left(3\sqrt{x}+2\right)+4}{3\sqrt{x}+2}\)
= \(2+\dfrac{4}{3\sqrt{x}+2}\)
Để A \(\in Z\)
<=> \(4⋮3\sqrt{x}+2\)
Ta có bảng: