Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
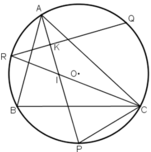
a) Gọi K là giao điểm của QR và AP.
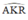là góc có đỉnh K nằm bên trong đường tròn
⇒ AP ⊥ QR.
+ R, P lần lượt là điểm chính giữa các cung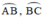 
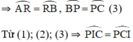
⇒ ΔPCI cân tại P.
Kiến thức áp dụng
+ Số đo của góc có đỉnh nằm bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+ Số đo của góc nội tiếp bằng một nửa số đo cung bị chắn.
a) Gọi giao điểm của AP và QR là K.
\(\widehat{AKR}\) là góc có đỉnh ở bên trong đường tròn nên
\(\widehat{AKR}\) = sđcung(AR +QC + CP)/2 =
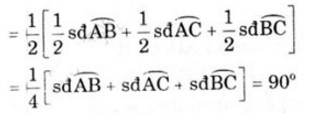
Vậy \(\widehat{AKR}\) = 900 hay AP \(\perp\) QR
b) \(\widehat{CIP}\) là góc có đỉnh ở bên trong đường tròn nên:
\(\widehat{CIP}\) = sđcung(AR +CP)/2 (1)
\(\widehat{PIC}\) góc nội tiếp, nên \(\widehat{PIC}\)= (sđ cung RB + BP)/2 (2)
Theo giả thiết thì cung AR = RB (3)
Cung CP = BP (4)
Từ (1), (2), (3), (4) suy ra: \(\widehat{CIP}\) = \(\widehat{PIC}\). Do đó \(\Delta\)CPI cân.
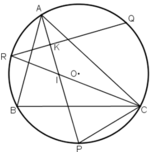
+ R, P lần lượt là điểm chính giữa các cung 
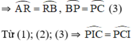
⇒ ΔPCI cân tại P.
M A B H O N I K C D O'
1) Xét đường tròn tâm O' đường kính AN: Điểm I thuộc (O') => ^AIN=900 => ^NIB=900
Xét tứ giác NHBI: ^NHB=^NIB=900 => Tứ giác NHBI nội tiếp đường tròn (đpcm).
2) Ta có tứ giác AKNI nội tiếp (O') => ^KAI+^KNI=1800 (1)
Tứ giác NHBI nội tiếp đường tròn (cmt) => ^INH+^IBH=1800 (2)
MA và MB là 2 tiếp tuyến của (O;R) => MA=MB => \(\Delta\)AMB cân tại M
=> ^MAB=^MBA hay ^KAI=^IBH (3)
Từ (1); (2) và (3) => ^KNI=^INH
Ta thấy: ^NKI=^NAI (Cùng chắn cung NI)
Theo t/c góc tạo bởi tiếp tuyến và dây cung => NAI=^NBH
=> ^NKI=^NBH. Mà ^NBH=^NIH (Cùng chắn cung HN) => ^NKI=^NIH
Xét \(\Delta\)NHI và \(\Delta\)NIK: ^NIH=^NKI; ^KNI=^INH (cmt) => \(\Delta\)NHI~\(\Delta\)NIK (g.g) (đpcm).
3) ^NIH=^NKI. Mà ^NKI=^NAI => ^NIH=^NAI hay ^NIC=^NAB (4)
^NIK=^NAK (Chắn cung NK). Mà ^NAK=^NBA (Góc tạo bởi tiếp tuyến và dây cung)
=> ^NIK=^NBA hay ^NID=^NBA (5)
Cộng (4) & (5) => ^NIC+^NID = ^NAB+^NBA = 1800 - ^ANB = 1800-^CND
=> ^CID+^CND=1800 => Tứ giác CNDI nội tiếp đường tròn => ^NDC=^NIC
Lại có: ^NIC=^NKI=^NAI => ^NDC=^NAI (2 góc đồng vị) => CD//AI hay CD//AB (đpcm).
#)Giải :
Bài 1 :
A B C O D E K
a) Các \(\Delta DBC;\Delta EBC\) nội tiếp đường tròn đường kính BC
\(\Rightarrow\Delta DBC;\Delta EBC\) vuông
\(\Rightarrow CD\perp AB;BE\perp AC\)
b) K là trục tâm của \(\Delta ABC\)
\(\Rightarrow AK\perp BC\)