Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Nối DD và FF
Xét ΔBDFΔBDF và ΔDEFΔDEF , ta có :
DF=DFDF=DF ( cạnh chung )
ˆBDF=ˆDEFBDF^=DEF^ ( vì AB//EFAB//EF )
ˆDFB=ˆFDEDFB^=FDE^ ( vì DE//BCDE//BC )
⇒ΔBDF=ΔFDE(g.c.g)⇒ΔBDF=ΔFDE(g.c.g)
⇒DB=EF⇒DB=EF ( hai cạnh tương ứng )
Mà AD=DB⇒AD=EFAD=DB⇒AD=EF
b. Xét ΔADEΔADE và ΔEFCΔEFC , ta có :
ˆA=ˆFECA^=FEC^ ( vì AB//EFAB//EF )
AD=EFAD=EF ( theo câu a )
ˆADE=ˆEFC(=ˆB)ADE^=EFC^(=B^)
⇒ΔADE=ΔEFC(g.c.g)

Answer:
Bài 1:
Vì AB = AC nên tam giác ABC cân tại A
=> Góc ABC = góc ACB = (180 độ - góc BAC) : 2 = 30 độ
Ta gọi DF là trung trực của AC
=> DF vuông góc AC = F; FC = FA
Mà DF là trung trực của AC
=> Góc ADA = 2 góc CDF = 2 . (180 độ - góc DCF - góc CFD) = 120 độ
Xét tam giác ACE và tam giác BAD:
BD = AE
AC = AB
Góc EAC = góc DBA = 30 độ
=> Tam giác ACE = tam giác BAD (c.g.c)
=> Góc CED = góc ADB = góc EDC = 180 độ - góc CDA = 60 độ
Bài 2:
Có: IK là trung trực của BC
=> IB = IC
Tương tự ID = IA mà AB = CD
=> Tam giác IAB = tam giác IDC (c.c.c)
=> Góc IAB = góc IDA = góc IAC
=> AI là tia phân giác của góc BAD
Mà AI là tia phân giác của góc A
IE vuông góc AB; IH vuông góc AC
=> IE = IH
\(\Rightarrow BE^2=IB^2-IE^2=IC^2-IH^2=HC^2\)
=> BE = HC
Mà IE = IH; góc IEA = góc IHA = 90 độ; góc EAI = góc IAH
=> Tam giác AEI = tam giác AHI (g.c.g)
=> AE = AH mà IE = IH
=> IA là trung trực của EH
Có: CF song song AB nên góc FHC = góc AHE = góc AEH = góc HFC
=> Tam giác CHF cân ở C
=> CF = CH
=> CF = BE
Mà KB = KC; góc EBK = góc KCF
=> Tam giác BKE = tam giác CKF (c.g.c)
=> Góc BKE = góc FKC
=> E, F, K thẳng hàng

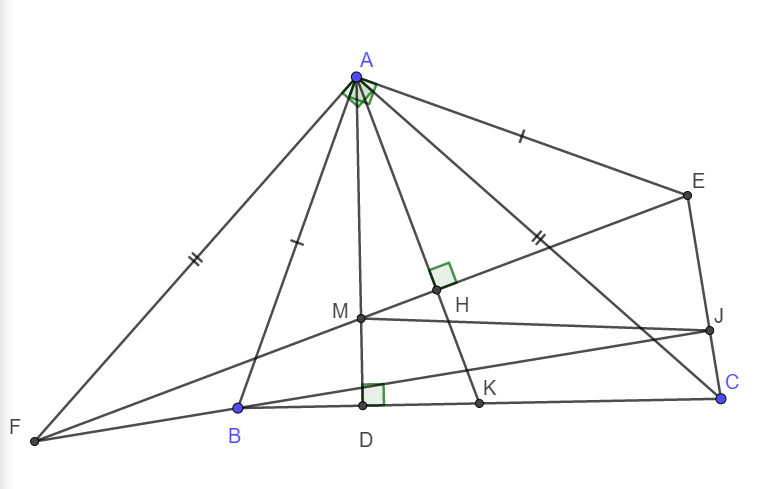
a) Xét tam giác ACK và tam giác FAM có :
AC = FA
\(\widehat{CAK}=\widehat{AFM}\) (Cùng phụ với góc \(\widehat{FAK}\) )
\(\widehat{ACK}=\widehat{FAM}\) (Cùng phụ với góc \(\widehat{DAC}\) )
\(\Rightarrow\Delta ACK=\Delta FAM\left(g-c-g\right)\)
b) Do \(\Delta ACK=\Delta FAM\left(cma\right)\Rightarrow FM=AK\)
Chứng minh hoàn toàn tương tự câu a ta có: \(\Delta ABK=\Delta EAM\left(g-c-g\right)\)
\(\Rightarrow ME=AK\)
Từ đó suy ra FM = ME hay M là trung điểm EF.
c) Kéo dài FB cắt EC tại J. Ta chứng minh \(\widehat{FJE}=90^o\)
Xét tam giác FAB và tam giác CAE có:
FA = CA
AB = AE
\(\widehat{FAB}=\widehat{CAE}\) (Cùng phụ với góc \(\widehat{BAC}\) )
\(\Rightarrow\Delta FAB=\Delta CAE\left(c-g-c\right)\)
\(\Rightarrow FB=CE\) và \(\widehat{AFB}=\widehat{ACE}\)
Xét tứ giác AFJE có:
\(\widehat{AFJ}+\widehat{FJE}+\widehat{JEA}+\widehat{EAF}=360^o\)
\(\Rightarrow\widehat{ACE}+\widehat{FJE}+\widehat{CEA}+\widehat{EAC}+90^o=360^o\)
\(\Rightarrow\widehat{FJE}+\widehat{ACE}+\widehat{CEA}+\widehat{EAC}=270^o\)
\(\Rightarrow\widehat{FJE}+180^o=270^o\)
\(\Rightarrow\widehat{FJE}=90^o\)
Vậy nên \(FB\perp EC\) (đpcm).
Bài 2:
A B C H I M N B' C' D E
a) Gọi giao điểm của đường phân giác ^ABC và ^ACB với AC và AB lần lượt là E và D
Dễ thấy: ^BAH=^ACB (Cùng phụ với ^HAC) => 1/2. ^BAH = 1/2. ^ACB
=> ^DAM=^ACD. Mà ^DAM+^MAC=^BAC=900 => ^ACD+^MAC=900 => AM \(\perp\)CD
hay NI\(\perp\)AM.
Tương tự ta chứng minh MI\(\perp\)AN
Xét tam giác MAN: NI\(\perp\)AM; MI\(\perp\)AN => I là trực tâm của tam giác MAN (đpcm).
b) Do I là trực tâm của tam giác AMN (cmt) => AI\(\perp\)MN hay AI\(\perp\)B'C'
Ta có: Tam giác ABC có 2 đường phân giác ^ABC và ^ACB cắt nhau tại I => AI là phân giác ^BAC
=> AI là phân giác ^B'AC'.
Xét tam giác AB'C': AI là phân giác ^B'AC'. Mà AI\(\perp\)B'C' => Tam giác AB'C' cân tại A
Lại có: ^B'AC'=900 => Tam giác B'AC' vuông cân tại A.

A B C D K M Q
a) b) cậu biết làm rồi nhé
c) Vì K là trung điểm cạnh BC ( gt )
\(\Rightarrow DK\)là trung tuyến cạnh BC.
Vì A là trung điểm của BD
\(\Rightarrow AC\)là trung tuyến cạnh BD
mà DK cắt AC tại M
\(\Rightarrow M\)là trọng tâm của tam giác BCD.
\(\Rightarrow MC=\frac{2}{3}AC\left(tc\right)\)
( BẠN TỰ THAY VÀO NHA )
d) Vì tam giác BCD cân ( cmt )
\(\Rightarrow BC=DC\left(đn\right)\)
Mà AC là trung tuyến của tam giác BCD ( cmt )
\(\Rightarrow AC\)cũng là đường phân giác của góc BCD .( tc)
\(\Rightarrow\widehat{BCA}=\widehat{DCA}=\frac{1}{2}\widehat{BCD}\)
Xét tam giác BCM và tam giác DCM có:
\(\hept{\begin{cases}CMchung\\BC=CD\left(cmt\right)\\\widehat{BCA}=\widehat{DCA}\left(cmt\right)\end{cases}\Rightarrow\Delta BCM=\Delta DCM\left(c-g-c\right)}\)
\(\Rightarrow\hept{\begin{cases}BM=DM\left(2canht.ung\right)\left(1\right)\\\widehat{CBM}=\widehat{CDM}\left(2goct.ung\right)\end{cases}}\)
Xét tam giác BMK và tam giác DMQ có:
\(\hept{\begin{cases}BM=DM\left(cmt\right)\\\widehat{CDM}=\widehat{CBM}\left(cmt\right)\\\widehat{BMK}=\widehat{QMD}\left(2gocdoidinh\right)\end{cases}\Rightarrow\Delta BMK=\Delta DMQ\left(g-c-g\right)}\)
\(\Rightarrow MK=MQ\left(2canht.ung\right)\left(2\right)\)
Vì M là trọng tâm của tam giác BCD (cmt) (4)
mà DK là trung tuyến của tam giác BCD (cmt)
\(\Rightarrow DM=2.MK\left(tc\right)\left(3\right)\)
Từ (1), (2) và (3) \(\Rightarrow BM=2.MQ\)
\(\Rightarrow BQ\)là trung tuyến của tam giác BCD (5)
Từ (4) và (5) \(\Rightarrow B,M,Q\)thẳng hàng

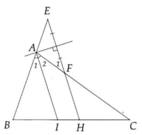
B C I H F E A
a)Ta có: BAI=CAI (AI là đường phân giác BAC)
Do:FH//AI=>CFH=CAI và BAI=AEF( đồng vị)
Mà:CFH=AFE(2 góc đối đỉnh)
Suy ra: AFE=AEF
Xét \(\Delta\)AFE:AFE=AEF=>\(\Delta\)AFE cân tại A=>Đường trung trực của EF đồng thời là đường cao
Hay:Đường trung trực của EF đi qua A
b) Như đã nói ở câu a:Đường trung trực của EF đồng thời là đường cao, giả sử ấy là AM
Ta có:AMF=90
Mà FH//AI=>AMF+MAI=180=>MAI=90=>AM\(\perp\)AI
Hay đường trung trực của EF vuông góc với AI
c)Do AI cố định nên đường trung trực của EF cố định
Mà \(\Delta\)AFE cân nên đường trung trực của EF đồng thời là đường trung tuyến ứng với EF
Hay đường trung tuyến ứng với EF cố định