Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha.
a,Xét tg ABE và tg HBE:
^BAE=^BHE=90*
^ABE=^HBE(BE là pg)
BE chung
=>tg ABE= tg HBE(ch-gn)
b,+,tg ABC có:^BAC=90*,^ABC=60*
=>^C=30*
+,tg BHE có: ^BHE=90*,^EBH=30*(^EHB=1/2ABC)
=>^HEB=60*
Mà HK // BE
=>^HBE=^EHK=60*(slt)
+, tg CHE có:^EHC=90*,^C=30*
=>HEC=60*
+,tg HEK có:
^EHK=60*,^HEC(^HEK)=60*
=>TG HEK đều(dhnb)
Phần c mik chỉ ghi các bước thôi còn bạn tự chình bày nhé.
c, +,CM:tg AEM=tg HEC(cgv-gnk)
=>AM=HC
+,CM:BM=BC
+,CM:tg BMI=tgBCI(cgc)
=>NM=NC
Xong r nha. Chúc bạn học tốt.

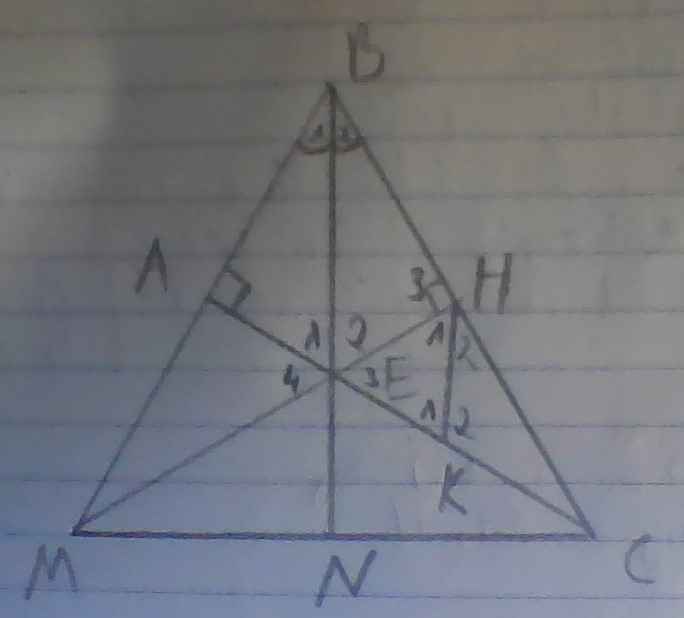
a) có BE là tia p/g của góc ABC
=> góc B1 = góc B2 = góc ABC/2 = 600 /2 = 300
có △ABC vuông tại A => △ABE vuông tại A
EH⊥BC=> △HBE vuông tại H
Xét △ vuông ABE và △vuông HBE có
góc B1 = góc B2
BE chung
=>△ vuông ABE =△vuông HBE ( cạnh huyền - góc nhọn)
b) có △ABE vuông tại A=> góc B1 + góc E1 = 900
góc E1 = 600 ( vì góc B1 = 300)
có △ vuông ABE =△vuông HBE
=> góc E1 = góc E2
mà HK//BE => góc E1 = góc K1 (ĐV)
và góc E2 = góc H1 (SLT)
=> góc E1 = góc E2 = góc K1=góc H1 = 600
=> △HEK đều
c) có góc E1 = góc E2 ; góc E3 = góc E4
=>góc E1 +góc E4 = góc E2 + góc E3
=> góc BEM= góc BEC
Xét △BEM và △ BEC có
góc B1 = góc B2
BE chung
góc BEM= góc BEC
=> △BEM = △ BEC (g.c.g)
=>BM=BC
=>△BMC cân tại B
trong △BMC có BN là đường p/g xuất phát từ đỉnh B
lại có △BMC cân tại B
=> BN cũng là đường trung tuyến xuất phát từ đỉnh B
=> N là trung điểm của MC
=> NM=NC

Bài 5:
a) Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABE=ΔHBE(cạnh huyền-góc nhọn)