Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

chứng minh: \(1+tg^2\alpha=\dfrac{1}{cos^2\alpha}\)
xét VT: \(1+tg^2\alpha=1+\dfrac{sin^2\alpha}{cos^2\alpha}\left(vì:tg\left(\alpha\right)=\dfrac{sin\left(\alpha\right)}{cos\left(\alpha\right)}\right)\)
\(=\dfrac{cos^2\alpha+sin^2\alpha}{cos^2\alpha}=\dfrac{1}{cos^2\alpha}\left(vì:sin^2\alpha+cos^2\alpha=1\right)=VP\Rightarrow1+tg^2\alpha=\dfrac{1}{cos^2\alpha}\)
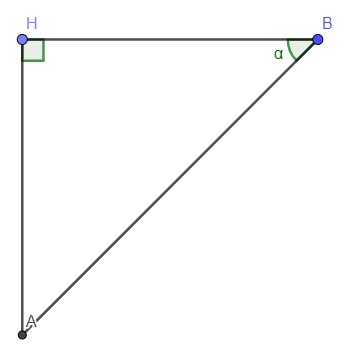
\(\Leftrightarrow1+\dfrac{AH^2}{50^2}=\dfrac{1}{\left(\dfrac{AH^2}{AB^2}\right)}=\dfrac{AB^2}{AH^2}\Leftrightarrow\dfrac{2500+AH^2}{2500}=\dfrac{AB^2}{AH^2}\Leftrightarrow2500AH^2+AH^4=2500AB^2\left(1\right)\)
ta có: \(AH^2+BH^2=AB^2\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow2500AH^2+AH^4=2500\left(AH^2+50^2\right)\Leftrightarrow AH^4=2500.2500=50^4\Leftrightarrow AH=50\left(m\right)\left(3\right)\)
\(\left(2\right)\left(3\right)\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{50^2+50^2}=50\sqrt{2}\left(m\right)\)
vậy chiều rộng con sông là: \(AH=50\left(m\right)\) và quãng đường đò đã đi là \(AB=50\sqrt{2}\left(m\right)\)

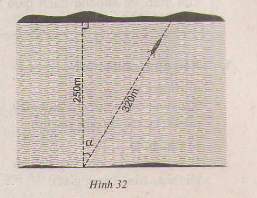
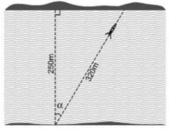
Chiếc đò lệch đi một góc bằng:
\(\cos\alpha=\frac{250}{320}\Rightarrow\alpha\approx38^o37'\)
Chiếc đò lệch đi một góc bằng:
250/320=~38`37(sấp xỉ 38 độ 37)
ĐS:....(Tự điền nha)

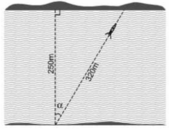
Lời giải:
Giả sử dòng nước đẩy chiếc đò lệch đi một góc $\alpha$
Ta có: $\cos \alpha=\frac{250}{320}=\frac{25}{32}$
$\Rightarrow \alpha=38,62^0$
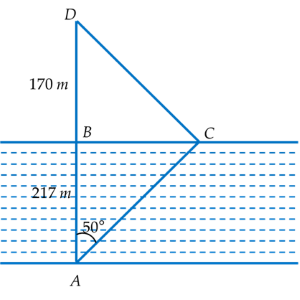

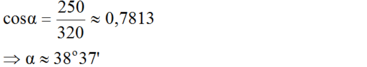
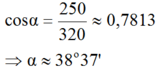
Trong tam giác vuông ABC:
\(cosA=\dfrac{AB}{AC}\Rightarrow AC=\dfrac{AB}{cosA}=\dfrac{217}{cos50^0}=337,6\left(m\right)\)
\(tanA=\dfrac{BC}{AB}\Rightarrow BC=AB.tanA=217.tan50^0=258,6\left(m\right)\)
Áp dụng định lý Pitago trong tam giác vuông BCD:
\(CD=\sqrt{BC^2+BD^2}=309,5\left(m\right)\)
Quãng đường mà Hùng đã đi là:
\(337,6+309,5=647,1\left(m\right)\)