Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

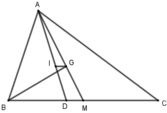
Gọi D, M là giao điểm của AI, AG với BC.
Vì AD là tia phân giác góc B A C ^ nên B D A B = D C A C (t/c)
⇒ B D 12 = D C 18 = B D + D C 12 + 18 = 15 30 = 1 2
=> BD = 12. 1 2 = 6, DC =18. 1 2 = 9
Lại có: BI là tia phân giác A B D ^ nên A I I D = A B B D = 12 6 = 2 (tính chất)
=> I D A D = M G M A = 1 3 hay D đúng
Mà AG = 2GM (vì G là trọng tâm)
Nên A I I D = A G G M = 2 hay B đúng
Theo định lí đảo của định lí Talet ta có:
IG // DM => IG // BC hay A đúng
Chỉ có C sai
Đáp án: C

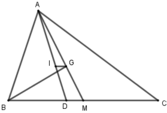
Do M là trung điểm BC nên MB = 1 2 BC = 1 2 .15 = 7,5 cm
Mà BD = 6cm nên DM = 7,5 cm – 6cm = 1,5 cm
Do IG // DM nên I G D M = A G A M = 2 3 => IG = 2 3 DM = 1 3 .1,5 = 1 cm
Đáp án: A

a) Gọi tam giác ACB có AN là phân giác và trung tuyến AM
\(\frac{NB}{NC}=\frac{AB}{AC}=\frac{6}{12}=\frac{1}{2}\)
\(\Rightarrow NB=\frac{NC}{2}\)
NC+NB=NC+0,5NC=1,5NC=BC=9 (cm) <=> NC=6cm
=>NB=3cm
Ta có: \(\frac{NB}{BC}=\frac{3}{9}=\frac{1}{3}\)
Xét tam giác ABN có BI là phân giác
=> \(\frac{AI}{IN}=\frac{BA}{BN}=\frac{6}{3}=2\)
Lại có AM là trung tuyến nên \(\frac{AG}{GM}=2\)
\(\Rightarrow\frac{AG}{GM}=\frac{AI}{IN}=2\)
=> IG//BC(Talet đảo) (đpcm)
b) \(BM=\frac{9}{2}=4,5\left(cm\right)\)
=> MN=4,5 -3=1,5 (cm)
\(\frac{AG}{AM}=\frac{2}{3}=\frac{IG}{MN}\)(Định lý Talet)
\(\Rightarrow\frac{2}{3}=\frac{IG}{1,5}\Rightarrow IG=1cm\)

Gọi E là giao điểm của BH và AC
AD là tia phân giác góc A
AH là đường cao của ΔABE
AH là tia phân giác của \(\widehat{BAE}\)
\(\Rightarrow\Delta ABE\) cân tại A
\(\Rightarrow AB=AE\)
Theo đề ra: AB = 12cm => AE = 12cm
\(EC=AC-AE=18-12=6cm\)
AH là đường cao của ΔABE cân tại A
=> AH là trung tuyến của ΔABE
=> H là trung điểm của BE
Ta có: M là trung điểm của BC
=> HM là đường trung bình của ΔBEC
\(\Rightarrow HM=\frac{EC}{2}=\frac{6}{2}=3cm\)
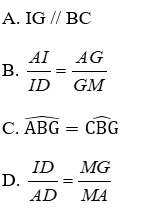
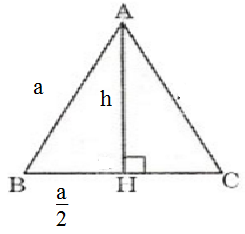
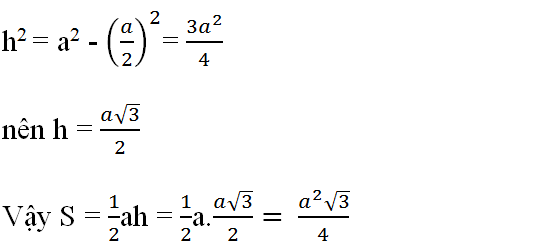
TK
Gọi D, M là giao điểm của AI, AG với BC.
Theo định lí đảo của định lí Talet ta có:
IG // DM ⇒ IG // BC hay A đúng
Chỉ có C sai
Đáp án cần chọn là: C
Chọn C