Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do tam giác ABC vuông tại A và \(\widehat{B}=30^o\) \(\Rightarrow C=60^o\)
\(\Rightarrow\left(\overrightarrow{AB},\overrightarrow{BC}\right)=150^o;\)\(\left(\overrightarrow{BA},\overrightarrow{BC}\right)=30^o;\left(\overrightarrow{AC},\overrightarrow{CB}\right)=120^o\)
\(\left(\overrightarrow{AB},\overrightarrow{AC}\right)=90^o;\left(\overrightarrow{BC},\overrightarrow{BA}\right)=30^o\).Do vậy:
a) \(\cos\left(\overrightarrow{AB},\overrightarrow{BC}\right)+\sin\left(\overrightarrow{BA},\overrightarrow{BC}\right)+\tan\frac{\left(\overrightarrow{AC},\overrightarrow{CB}\right)}{2}\)
\(=\cos150^o+\sin30^o+\tan60^o\)
\(=-\frac{\sqrt{3}}{2}+\frac{1}{2}+\sqrt{3}\)
\(=\frac{\sqrt{3}+1}{2}\)
b) \(\sin\left(\overrightarrow{AB},\overrightarrow{AC}\right)+\cos\left(\overrightarrow{BC},\overrightarrow{AB}\right)+\cos\left(\overrightarrow{CA},\overrightarrow{BA}\right)\)
\(=\sin90^o+\cos30^o+\cos0^o\)
\(=1+\frac{\sqrt{3}}{2}\)
\(=\frac{2+\sqrt{3}}{2}\)

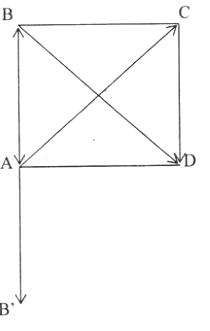
A B C D B' O
\(cos\left(\overrightarrow{AC};\overrightarrow{BA}\right)=cos\left(\overrightarrow{AC};\overrightarrow{AB'}\right)=cos\widehat{CAB'}=cos135^o\)\(=\dfrac{\sqrt{2}}{2}\).
\(sin\left(\overrightarrow{AC};\overrightarrow{BD}\right)=sin90^o=1\) do \(AC\perp BD\).
\(cos\left(\overrightarrow{AB};\overrightarrow{CD}\right)=cos180^o=-1\) do hai véc tơ \(\overrightarrow{AB};\overrightarrow{CD}\) ngược hướng.

1/ Tinh ∆. Pt co 2 nghiem x1,x2 <=> ∆>=0.
Theo dinh ly Viet: S=x1+x2=-b/a=m+3.
Theo gt: |x1|=|x2| <=> ...
2/ \(\frac{\sin^2x-\cos^2x}{1+2\sin x.\cos x}\)
\(=\frac{\cos^2x\left(\frac{\sin^2x}{\cos^2x}-\frac{\cos^2x}{\cos^2x}\right)}{\cos^2x\left(\frac{1}{\cos^2x}+\frac{2\sin x.\cos x}{\cos^2x}\right)}\)
\(=\frac{\tan^2x-1}{\tan^2x+1+2\tan x}\)
\(=\frac{\left(\tan x-1\right)\left(\tan x+1\right)}{\left(\tan x+1\right)^2}\)
\(=\frac{\tan x-1}{\tan x+1}\left(dpcm\right)\)
c/ A M C B N BC=8 AC=7 AB=6
- Ta có: \(\overrightarrow{BA}^2=\left(\overrightarrow{CA}-\overrightarrow{CB}\right)^2\)
\(\Leftrightarrow BA^2=CA^2-2\overrightarrow{CA}.\overrightarrow{CB}+CB^2\)
\(\Leftrightarrow\overrightarrow{CA}.\overrightarrow{CB}=\frac{CA^2+CB^2-BA^2}{2}=\frac{77}{2}\)
- \(\overrightarrow{MN}^2=\left(\overrightarrow{CN}-\overrightarrow{CM}\right)^2=\left(\frac{3}{2}\overrightarrow{CB}-\frac{5}{7}\overrightarrow{CA}\right)^2\)
\(\Leftrightarrow MN^2=\frac{9}{4}CB^2-\frac{15}{7}\overrightarrow{CA}.\overrightarrow{CB}+\frac{25}{49}CA^2\)
\(=\frac{9}{4}.64-\frac{15}{7}.\frac{77}{2}+\frac{25}{49}.49\)
\(=\frac{173}{2}\)
\(\Rightarrow MN=\sqrt{\frac{173}{2}}=\frac{\sqrt{346}}{2}\)

Câu a)
Từ \(\tan a=3\Leftrightarrow \frac{\sin a}{\cos a}=3\Rightarrow \sin a=3\cos a\)
Do đó:
\(\frac{\sin a\cos a+\cos ^2a}{2\sin ^2a-\cos ^2a}=\frac{3\cos a\cos a+\cos ^2a}{2(3\cos a)^2-\cos ^2a}\)
\(=\frac{\cos ^2a(3+1)}{\cos ^2a(18-1)}=\frac{4}{17}\)
Câu b)
Có: \(\cot \left(\frac{\pi}{2}-x\right)=\tan x=\frac{\sin x}{\cos x}\)
\(\cos\left(\frac{\pi}{2}+x\right)=-\sin x\)
\(\Rightarrow \cot \left(\frac{\pi}{2}-x\right)\cos \left(\frac{\pi}{2}+x\right)=\frac{-\sin ^2x}{\cos x}\)
Và:
\(\frac{\sin (\pi-x)\cot x}{1-\sin ^2x}=\frac{\sin x\cot x}{\cos^2x}=\frac{\sin x.\frac{\cos x}{\sin x}}{\cos^2x}=\frac{1}{\cos x}\)
Do đó:
\(\Rightarrow \cot \left(\frac{\pi}{2}-x\right)\cos \left(\frac{\pi}{2}+x\right)+\frac{\sin (\pi-x)\cot x}{1-\sin ^2x}=\frac{1-\sin ^2x}{\cos x}=\frac{\cos ^2x}{\cos x}=\cos x\)
Ta có đpcm.

a) \(sin\left(x+\dfrac{\pi}{2}\right)=cos\left[\dfrac{\pi}{2}-\left(x+\dfrac{\pi}{2}\right)\right]=cos\left(-x\right)=cosx\)
a : Đúng.
b) \(cos\left(x+\dfrac{\pi}{2}\right)=sin\left[\dfrac{\pi}{2}-\left(x+\dfrac{\pi}{2}\right)\right]=sin\left(-x\right)=-cosx\)
b: Sai.
c) \(sin\left(x-\pi\right)=-sin\left(\pi-x\right)=-sinx\).
d: Sai.
d) \(cos\left(x-\pi\right)=cos\left(\pi-x\right)=cosx\)
c: Đúng.
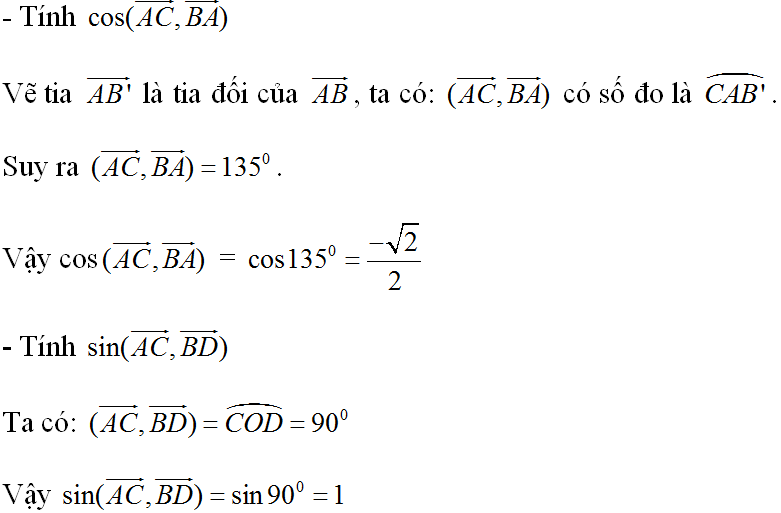
a.
\(P=cos120^0+cos120^0+cos120^0=-\dfrac{3}{2}\)
b.
\(A=\dfrac{\dfrac{sinx}{cosx}-\dfrac{cosx}{cosx}}{\dfrac{sinx}{cosx}+\dfrac{cosx}{cosx}}=\dfrac{tanx-1}{tanx+1}=\dfrac{2-1}{2+1}=\dfrac{1}{3}\)
c.
\(A=\dfrac{cos\left(720+30\right)+sin\left(360+60\right)}{sin\left(-360+30\right)-cos\left(-360-30\right)}=\dfrac{cos30+sin60}{sin30-cos30}=-3-\sqrt{3}\)