Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(C=\left[\left(u^2y^4\right)^2\right]^2+4u^4y^8+4\)
\(=\left(u^4y^8\right)^2+4u^4y^8+4\)
\(=\left(u^4y^8+2\right)^2\)
\(C=4u^4v^8+\left(u^2v^4\right)^4+4\)
\(C=\left(u^4v^8\right)^2+2.u^4v^8.2+2^2\)
\(C=\left(u^4v^8+2\right)^2\)
Chúc bạn học tốt~

Bài giải:
a) – x3 + 3x2– 3x + 1 = 1 – 3 . 12 . x + 3 . 1 . x2 – x3
= (1 – x)3
b) 8 – 12x + 6x2 – x3 = 23 – 3 . 22. x + 3 . 2 . x2 – x3
= (2 – x)3

Mình lp 7 -_-
Mình giải thích rõ hơn nhé :
Đặt (2x + 3y) là a, đa thức được viết thành :
\(a^2+2a+1=a^2+2a\cdot1+1^2=\left(a+1\right)^2\)
Sau đó thế 2x + 3y = a vào là ra.
\(\left(2x+3y\right)^2+2\cdot\left(2x+3y\right)+1\)
\(=\left(2x+3y+1\right)^2\)

a) -x3 + 3x2 - 3x + 1
= -(x3 - 3x2 + 3x - 1)
=-(x - 1)3
b) 8 - 12x + 6x2 - x3
= 23 - 3.22.x + 3.2.x2 - x3
= (2 - x)3

\(C=4u^4v^8+\left(u^2v^4\right)^4+4\)
\(C=\left(u^4v^8\right)^2+2.u^4v^8.2+2^2\)
\(C=\left(u^4v^8+2\right)^2\)
C= 4u4v8 + ( u2v4)4 +4
= (u4v8)2 +2.u4v8.2 + 22
= ( u4v8+2)2

a) \(9x^2+6x+1=\left(3x+1\right)^2\)
b)\(x^2-x+\frac{1}{4}=\left(x-\frac{1}{2}\right)^2\)
c)\(x^2y^4-2xy^2+1=\left(xy^2-1\right)^2\)
d) \(x^2+\frac{2}{3}x+\frac{1}{9}=\left(x+\frac{1}{3}\right)^2\)
a) 9x2 + 6x + 1 = ( 3x + 1 )2
b) x2 - x + 1/4 = ( x - 1/2)2
c) x2 . y4 - 2xy2 + 1 = ( xy2 - 1 ) 2
d) x2 + 2/3x + 1/9 = (x+1/3)2
Viết biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu :
xy2 + \(\frac{1}{4}x^2y^4\)+ 1

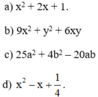
a) x2 + 2x + 1
= x2 + 2.x.1 + 12
= (x + 1)2 (Áp dụng hằng đẳng thức (1) với A = x và B = 1)
b) 9x2 + y2 + 6xy
= 9x2 + 6xy + y2
= (3x)2 + 2.3x.y + y2
= (3x + y)2 (Áp dụng hằng đẳng thức (1) với A = 3x và B = y)
c) 25a2 + 4b2 – 20ab
= 25a2 – 20ab + 4b2
= (5a)2 – 2.5a.2b + (2b)2
= (5a – 2b)2 (Áp dụng hằng đẳng thức (2) với A = 5a và B = 2b)
(Áp dụng hằng đẳng thức (2) với A = x và B = 1/2 )