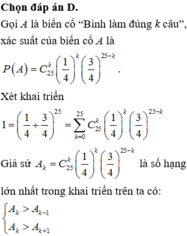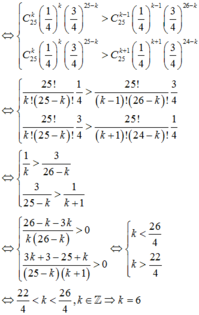Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số phần tử của không gian mẫu là n Ω = C 30 5 = 142506
Gọi A là biến cố: “đề thi lấy ra là một đề thi tốt”.
Vì trong một đề thi “tốt” có cả ba câu dễ, trung bình và khó đồng thời số câu dễ không ít hơn 2 nên ta xét các trường hợp sau:
Trường hợp 1: Đề thi gồm 3 câu dễ, 1 câu trung bình và 1 câu khó có C 15 1 C 10 1 C 5 1 cách.
Trường hợp 2: Đề thi gồm 2 câu dễ, 2 câu trung bình và 1 câu khó có C 15 2 C 10 2 C 5 1 cách.
Trường hợp 3: Đề thi gồm 2 câu dễ, 1 câu trung bình và 2 câu khó có C 15 2 C 10 1 C 5 2 cách.
Suy ra n A = C 15 3 C 10 1 C 5 1 + C 15 2 C 10 2 C 5 1 + C 15 2 C 10 1 C 5 2 = 56875
Vậy xác suất cần tìm là P A = n A n Ω = 56875 142506 = 625 1566
Đáp án D

Đáp án A
Với 10 câu hỏi trắc nghiệm sẽ có 4 10 cách chọn đáp án.
Và bài điền tiếp theo chắc chắn sẽ giống 1 trong 4 10 bài điền trước đó.
Vậy có tất cả 4 10 + 1 = 1048577 phiếu thỏa mãn yêu cầu bài toán.

Gọi độ dài của tấm vải thứ 3 là a(m)
Theo bài ra ta có PT:
a-\(\frac{60,5+71,3+a}{3}\)=2,4
Giải Pt bằng máy tính ta được a=69,5
Vậy tấm vải thứ 3 dài 69,5m

Đáp án A
Với 10 câu trắc nghiệm sẽ có 4 10 cách chọn đáp án.
Và bài điền tiếp theo chắc chắn sẽ giống 1 trong 4 10 bài điền trước đó.
Vậy có tất cả 4 10 + 1 = 1048577 phiếu thỏa mãn yêu cầu bài toán.

2x-\(\frac{1}{3}\)=1-\(\frac{5}{6}\)
2x-\(\frac{1}{3}\)=\(\frac{1}{6}\)
2x=\(\frac{1}{6}\)+\(\frac{1}{3}\)
2x=1/6 +2/6
2x=\(\frac{1}{2}\)
x=1/2 : 2
x/\(\frac{1}{4}\)
\(\frac{7}{9}\):(2+\(\frac{3}{4}\)x)+\(\frac{5}{9}\)=\(\frac{23}{27}\)
7/9 :(2+3/4x)=\(\frac{23}{27}\)-\(\frac{5}{9}\)
7/9 :(2+3/4x)=\(\frac{23}{27}\)-\(\frac{15}{27}\)
7/9 :(2+3/4x)=\(\frac{8}{27}\)
(2+3/4x) =\(\frac{7}{9}\) . \(\frac{27}{8}\)
(2+3/4x) =\(\frac{21}{8}\)
\(\frac{3}{4}\)x =\(\frac{21}{8}\)-2
3/4x =21/8 -16/8
3/4x = 5/8
x =\(\frac{5}{8}\) : \(\frac{3}{4}\)
x =5/8 . 4/3
x =\(\frac{20}{24}\)