Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B. Có vật kính với tiêu cự vài chục cm như các máy ảnh chụp xa
Vì bất kì máy ảnh nào đều có vật kính và tiêu cự của nó không thể là chục m hay hàng km vì quá lớn so với kích thước của các vệ tinh.

Xét tg ABO \(\sim\Delta A'B'O\)
\(\dfrac{AB}{A'B'}=\dfrac{AO}{A'O}\)=>A'O \(=\dfrac{A'B'.AO}{AB}\)=\(\dfrac{3.2}{1,2}\)=5 (m)(1)
Vậy ảnh cách tk 1 khoảng bằng 5m
Xét tam giác OIF' đồng dạng vs tg A'B'F'
\(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'F'}\)=\(\dfrac{OF'}{A'O-OF'}\)
mà OI = AB = 1,2 m nên
\(\dfrac{AB}{A'B'}=\dfrac{OF'}{A'O-OF'}\)(2)
Từ (1) và (2) suy ra \(\dfrac{AO}{A'O}\)=\(\dfrac{OF'}{A'O-OF'}\)
=>AO(A'O-OF')=OF'. AO
=> 2.(5-OF')=OF'.2
=> 10 -2OF'=2OF'
=> OF'=2,5 (m)
Vậy tiêu cự của TK là 2,5m
+ Từ B vẽ tia tới đi qua quang tâm O cho tia ló tiếp tục truyền thẳng
+ Từ B vẽ tia tới song song vs trục chính cho tia ló đi qua tiêu điểm F'
+ Tia ló thứ nhất và tia ló thứ 2 giao nhau tại một điểm thì điểm đó là B'
+ Từ B' hạ vuông góc xuống trục chính ta đc A'

MÌNH THAM KHẢO NHÉ
a) Xét △ABO và △A′B′O có:
ABOˆ=A′B′Oˆ=900
BOAˆ=B′OA′ˆ (hai góc đối đỉnh)
⇒ Hai tam giác ABO và A'B'O là hai tam giác đồng dạng
⇒ \(\frac{A'B'}{AB}=\frac{B'O}{BO}\)
⇒ Độ phóng đại ảnh \(k=\frac{A'B'}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Tương tự: Hai tam giác A'B'F' và IOF' là hai tam giác đồng dạng
⇒\(\text{ }\frac{B'F'}{OF'}=\frac{A'B'}{IO}=\frac{d'}{d}\)
Áp dụng tính chất của tỉ lệ thức: \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)
⇒\(\frac{1}{f}=\frac{1}{d}=\frac{1}{f'}\)
CÓ MẤY CÁI KÍ HIỆU GÓC, MÌNH KHÔNG BIẾT VIẾT, BẠN THÔNG CẢM
a) Xét \(\Delta ABO\) và \(\Delta A'B'O'\)
\(ABO=A'B'O=90^0\)
\(BOA=B'O'A\)( hai góc đối đỉnh )
\(\Rightarrow\)Hai tam giác ABO và A'B'O là hai tam giác đồng dạng
\(\Rightarrow\frac{A'B}{AB}=\frac{B'O}{BO}\)
\(\Rightarrow\)Độ phóng đại ảnh : \(k=\frac{A'B}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Tương tự : Hai tam giác A'B'F và IOF' là hai tam giác đồng dạng
\(\Rightarrow\frac{B'F'}{OF}=\frac{A'B}{TO}=\frac{d'}{d}\)
Dựa vào tính chất của tỉ lệ thức : \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)

a) vì là TKHT mà theo đề thì ta có d (tức là OA) < f ,=> ảnh ảo, cùng chiều và lớn hơn vật
b)Xét tam giác OAB đồng dạng vs ta, giác OA'B'
=> h/h' = d/d' (AB/A'B'=OA/OA')..........(1)
xét tam giac F'OI đồng dạng vs tgiac F'A'B'
=> h/h' = f/(f+d') (( OI/A'B' = FO/(FO+FA')))..........(2)
từ 1 và 2 => d/d' =f/(f+d')
chia 2 vế cho dd'f => 1/d =1/f + 1/d'
theo đề có d và f => d'=12
thế d'=12, d=6, h=1 vào (1)
=>h'=2
F' A O A' B' I

Ta có: Để thu được ảnh thật ngược chiều, nhỏ hơn vật => vật phải cách thấu kính một khoảng d > 2f
Theo đầu bài ta có:
f = 16cm→2f = 32cm
=> Để thu được ảnh nhỏ hơn vật => vật cần đặt cách thấu kính một khoảng
d > 32cm
Đáp án: D

Đáp án: C
Khi chụp ảnh thì ảnh của vật trên phim là ảnh thật
Áp dụng công thức:
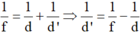
Khoảng cách giữa vật kính và phim là:
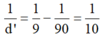
=> d' = 10 (cm)

a, Vẽ ảnh A'B'
A B A' B' F F' O I
b,
Gọi khoảng cách từ AB đến thấu kính là d, từ A'B' đến thấu kính là d'
Xét \(\Delta ABO \sim \Delta A'B'O\)
\(\Rightarrow \dfrac{AB}{A'B'}=\dfrac{BO}{B'O}=\dfrac{10}{d'}\)(1)
Xét \(\Delta IOF \sim \Delta A'B'F\)
\(\Rightarrow \dfrac{IO}{A'B'}= \dfrac{OF}{B'F}\)
Ta có: \(IO=AB\)
\(\Rightarrow \dfrac{AB}{A'B'}= \dfrac{14}{d'+14}\)(2)
Từ (1) và (2) \(\Rightarrow\dfrac{10}{d'}=\dfrac{14}{d'+14}\)
\(\Rightarrow d'=35cm\)
Vậy ảnh cách thấu kính 35 cm
Thế vào (1) ta được: \(\Rightarrow \dfrac{AB}{A'B'}=\dfrac{10}{35}\Rightarrow A'B' = \dfrac{35.2}{10}=7(cm)\)
Vậy ảnh cao 7cm.
Chọn B. Có vật kính. Tiêu cự của nó chỉ vào khoảng vài milimet.
Vì với máy ảnh nào cũng đều có vật kính và tiêu cự của nó không thể là vài cm hay chục cm vì quá lớn nên tiêu cự chỉ vào khoảng vài milimet.