Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án : A
Nếu chọn đề tài về lịch sử kháng chiến có 8 cách.
Nếu chọn đề tài về thiên nhiên có 7 cách.
Nếu chọn đề tài về con người có 10 cách.
Nếu chọn đề tài về văn hóa có 6 cách.
Nếu chọn đề tài di tích lịch sử có 5 cách.
Theo qui tắc cộng, ta có 8+7+10+5=36 cách chọn.

Đáp án A
Lấy ngẫu nhiên từ ngân hàng đề thi 4 câu hỏi để lập một đề thi
có C 20 4 = 4845 đề thi.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 2 câu đã thuộc
có C 10 2 . C 10 2 = 2025 trường hợp.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 3 câu đã thuộc
có C 10 3 . C 10 1 = 1200 trường hợp.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 4 câu đã thuộc
có C 10 4 = 210 trường hợp.
Do đó, thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc
có 2025 + 1200 + 210 = 3435 trường hợp.
Vậy xác suất để thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc là
3435 4845 = 229 323

Đáp án A
Lấy ngẫu nhiên từ ngân hàng đề thi 4 câu hỏi để lập một đề thi có C 20 4 = 4845 đề thi.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 2 câu đã thuộc
có C 10 2 . C 10 2 = 2025 trường hợp.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 3 câu đã thuộc
có C 10 3 . C 10 1 = 1200 trường hợp.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 4 câu đã thuộc
có C 10 4 = 210 trường hợp.
Do đó, thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc
có 2025 + 1200 +210 =3435 trường hợp.
Vậy xác suất để thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc là
3435 4845 = 229 323

Số cách chia 14 tiết mục thành 2 nhóm là: \(n(\Omega )= C_{14}^{7}.C_{7}^{7} \)
Gọi A là biến cố 2 tiết mục của lớp 12a1 được biểu diễn cùng một nhóm.
Số cách chọn 1 trong 2 nhóm để xếp 2 tiết mục của lớp 12a1 vào là: \( C_{2}^{1}\)
Số cách xếp 12 tiết mục còn lại là: \(C_{12}^{5}.C_{7}^{7}\)
Ta có \(n(A)= C_{2}^{1}.C_{12}^{5}.C_{7}^{7} \)
Xác suất xảy ra A là: \(P(A)= \frac{n(A)}{n(\Omega )} = \frac{C_{2}^{1}.C_{12}^{5}.C_{7}^{7}}{C_{14}^{7}.C_{7}^{7} } = \frac{6}{13} \)

Không gian mẫu: \(C_{20}^5.C_{15}^5.C_{10}^5\)
Chọn nhóm cho 5 bạn nữ: có 4 cách
Xếp 15 bạn nam vào 3 nhóm còn lại: \(C_{15}^5.C_{10}^5\)
Xác suất: \(P=\dfrac{4.C_{15}^5.C_{10}^5}{C_{20}^5.C_{15}^5.C_{10}^5}\)

Đáp án D
Mỗi cách chọn là một tổ hợp chập 5 của 15 nên ![]()
Số cách chọn là
![]()
Xác suất cần tìm là: ![]()

Đáp án A
Ta xét 2 trường hợp
TH1:
Đề thi có 9 câu hỏi nằm trong 25 câu mà học sinh nắm được
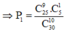
TH2:
Đề thi có 10 câu hỏi nằm trong 25 câu mà học sinh nắm được
![]()
Vậy xác suất cần tính là
![]()

Nếu chọn đề tài về lịch sử có 8 cách.
Nếu chọn đề tài về thiên nhiên có 7 cách.
Nếu chọn đề tài về con người có 10 cách.
Nếu chọn đề tài về văn hóa có 6 cách.
Theo qui tắc cộng, ta có 8+ 7+ 10 + 6 = 31 cách chọn.
Chọn đáp án C.