Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề bài , ta có phương trình : 2x + 150 = 500
\(\Leftrightarrow2x=500-150\)
\(\Leftrightarrow2x=350\)
\(\Leftrightarrow x=175\)

a) Trên đĩa cân bên trái ta thấy có 4 quả cân, có 3 quả có khối lượng \(x\) gam và 1 quả có khối lượng 100 gam nên khối lượng đĩa cân bên trái là: \(x + x + x + 100\) (gam)
Trên đĩa cân bên phải ta thấy có 2 quả cân, 1 quả có khối lượng \(x\) gam và một quả có khối lượng 400 gam nên khối lượng đĩa cân bên phải là: \(x + 400\) gam.
Từ điều kiện cân thăng bằng ta có biểu thức mối quan hệ sau:
\(x + x + x + 100 = x + 400\) hay \(3x + 100 = 400 + x\).
Vậy phương trình biểu diễn sự thăng bằng là \(3x + 100 = 400 + x\).
b) Nếu \(x = 100\) thì khối lượng đĩa cân bên trái là: \(3.100 + 100 = 300 + 100 = 400\) (gam); khối lượng đĩa cân bên phải là \(400 + 100 = 500\) (gam).
Do đó, cân không thăng bằng.
Nếu \(x = 150\) thì khối lượng đĩa cân bên trái là: \(3.150 + 100 = 550\) (gam); khối lượng đĩa cân bên phải là \(150 + 400 = 550\) (gam).
Do đó, cân thăng bằng.

Cân nặng của đĩa thứ nhất là: \(500\) g
Cân nặng của đĩa thứ hai là: \(2.x + 3.50 = 2x + 150\)
Phương trình biểu thị sự thăng bằng của cân là: \(2x + 150 = 500\).

gọi x là tổng số trứng (x>0,x thuộc N*)
ngày đàu bán được số trứng là (x-150) + \(\frac{1}{9}\left(x-150\right)\) =\(\frac{400}{3}+\frac{1}{9}x\)=> số trứng còn lại sau ngày thứ nhất bán là \(x-\frac{400}{3}-\frac{1}{9}x\)=\(\frac{8}{9}x-\frac{400}{3}\)
ngày thứ hai bán được số trứng là\(200+\frac{1}{9}\left(\frac{8}{9}x-\frac{400}{3}-200\right)\)=> số trứng còn lại sau ngày thứ hai bán là \(\frac{8}{9}x-\frac{400}{3}\)\(-\left(200+\frac{1}{9}\left(\frac{8}{9}x-\frac{400}{3}-200\right)\right)\)
tương tự nhé bn sau đó có phương trình x= ngày thứ 1 + 2 + 3 =>x=.... tự tính nha mình lười
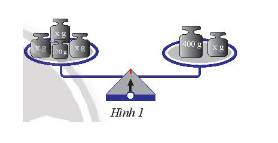
Nếu gói hàng là x (g) thì việc làm của cô bán hàng thể hiện bởi phương trình 2x + 150 = 500
500