Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
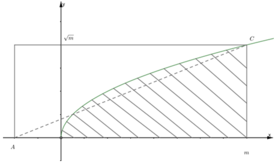
Phương pháp: Sử dụng tích phân.
Cách giải: Diện tích phần gạch chéo là

Vậy m=3 thỏa mãn yêu cầu bài toán.

Lời giải:
a) Gọi phương trình đường thẳng có dạng $y=ax+b$ $(d)$
Vì \(B,C\in (d)\Rightarrow \left\{\begin{matrix} 3=2a+b\\ -3=-4a+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=1\\ b=1\end{matrix}\right.\Rightarrow y=x+1\)
Vậy PT đường thẳng chứa cạnh $BC$ có dạng $y=x+1$
b) Tương tự, ta lập được phương trình đường thẳng chứa cạnh $AC$ là \((d_1):y=\frac{2x}{5}-\frac{7}{5}\).
Gọi PT đường cao đi qua $B$ của tam giác $ABC$ là \((d'):y=ax+b\)
Vì \((d')\perp (d_1)\Rightarrow \frac{2}{5}a=-1\Rightarrow a=\frac{-5}{2}\).
Mặt khác \(B\in (d')\Rightarrow 3=\frac{-5}{2}.2+b\Rightarrow b=8\)
\(\Rightarrow (d'):y=\frac{-5x}{2}+8\)
c) Gọi điểm thỏa mãn ĐKĐB là $M(a,b)$
Ta có: \(M\in (\Delta)\Rightarrow 2a+b-3=0\) $(1)$
$M$ cách đều $A,B$ \(\Rightarrow MA^2=MB^2\Rightarrow (a-1)^2+(b+1)^2=(a-2)^2+(b-3)^2\)
\(\Leftrightarrow 2-2a+2b=13-4a-6b\)
\(\Leftrightarrow 11-2a-8b=0(2)\)
Từ \((1);(2)\Rightarrow \left\{\begin{matrix} a=\frac{13}{14}\\ b=\frac{8}{7}\end{matrix}\right.\Rightarrow M\left ( \frac{13}{14};\frac{8}{7} \right )\)
con nếu đề bài cho 1 điểm và phương trình đường thẳng của tam giác muốn tìm phương trình đường cao còn lại vầ các cạnh thj làm thế nào

Câu 1:
\(AB=\sqrt{\left[3-\left(-2\right)\right]^2+\left(3-2\right)^2}=\sqrt{26}\)
\(BC=\sqrt{\left(2-3\right)^2+\left(-2-3\right)^2}=\sqrt{26}\)
\(AC=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-2-2\right)^2}=4\sqrt{2}\)
\(P=\dfrac{AB+BC+AC}{2}=\dfrac{2\sqrt{26}+4\sqrt{2}}{2}=\sqrt{26}+2\sqrt{2}\)
\(S=\sqrt{\left(\sqrt{26}+2\sqrt{2}\right)\cdot2\sqrt{2}\cdot2\sqrt{2}\cdot\left(\sqrt{26}-2\sqrt{2}\right)}=\sqrt{18\cdot8}=12\left(đvdt\right)\)

b: Thay x=2 vào (P), ta được:
\(y=-\dfrac{1}{4}\cdot2^2=-1\)
Vì (d) đi qua O(0;0) và A(2;-1) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}a\cdot0+b=0\\2a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{2}\\b=0\end{matrix}\right.\)

Ta có Pt d2 :x+2y-5=0
vì M ϵ d1 :x-y-1=0 nên M(m,m-1)
MA2 = (-1-m)2 + (2-m+1)2 = 1+2m+m2 +9-6m+m2 =2m2 -4m+10
<=> MA=\(\sqrt{2m^2-4m+10}\)
d(m,d2 )= \(\frac{\left|m+2m-2-5\right|}{\sqrt{1^2+2^2}}\) =\(\frac{\left|3m-7\right|}{\sqrt{5}}\)
theo bài ra thì MA=d(M,d2)
=>\(\frac{\left|3m-7\right|}{\sqrt{5}}\)=\(\sqrt{2m^2-4m+10}\) <=>|3m-7|=\(\sqrt{5}\)\(\sqrt{2m^2-4m+10}\)
<=>9m2 -42m +49=5(2m2-4m+10)
<=>9m2 -42m +49=10m2 -20m +50
<=>m2 +22m +1=0
<=>m= -11+2\(\sqrt{30}\) hoặc m=-11-2\(\sqrt{30}\)
=> M(-11+2\(\sqrt{30}\) ,-12+2\(\sqrt{30}\) ) hoặc M(-11-2\(\sqrt{30}\) ,-12-2\(\sqrt{30}\) )

a) vẽ dễ lắm ; tự vẽ nha
b) xét phương trình hoành độ của 2 đồ thị đó
ta có : \(x^2=-2x+3\Leftrightarrow x^2+2x-3=0\)
ta có : \(a+b+c=1+2-3=0\)
\(\Rightarrow\) phương trình có 2 nghiệm phân biệt
\(x_1=1\) \(\Rightarrow y=x^2=1^2=1\) vậy \(A\left(1;1\right)\)
\(x_2=\dfrac{c}{a}=-3\) \(\Rightarrow y=x^2=\left(-3\right)^2=9\) vậy \(B\left(-3;9\right)\)
vậy 2 đồ thị cắt nhau tại 2 điểm phân biệt là \(A\left(1;1\right)\) và \(B\left(-3;9\right)\)
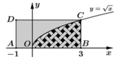
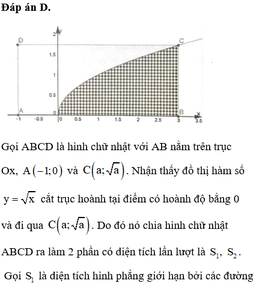


Từ hình vẽ ta suy ra B(a;0)
Hình chữ nhật ABCD có AB = a + 1 và AD = a nên có diện tích S = a (a+1)
Diện tích miền gạch sọc: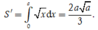
Theo giả thiết, ta có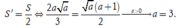
Chọn B.