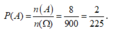Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi \(\overrightarrow{u},\overrightarrow{v}\) theo thứ tự là vec tơ chỉ phương đơn vị của các tia Ox, Oy, tương ứng cùng hướng với các tia Ox, Oy gọi I là tâm của \(\omega\). Chọn O làm gốc vec tơ điểm và với mỗi điểm X của mặt phẳng, ký hiệu \(\overrightarrow{x}\) để chỉ vec tơ \(\overrightarrow{OX}\). Trung trực OA cắt các đường thẳng \(d_1,d_2\) theo thứ tự tại B, C.
Khi đó B, C cố định và do I nằm trên đường thẳng BC nên \(\overrightarrow{i}=\alpha\overrightarrow{b}+\left(1-\alpha\right)\overrightarrow{c}\)
Mặt khác , theo định lí chiếu ta có :
\(\overrightarrow{m}=2\left(\overrightarrow{i}.\overrightarrow{u}\right).\overrightarrow{u}\) và \(\overrightarrow{n}=2\left(\overrightarrow{i}.\overrightarrow{v}\right).\overrightarrow{v}\)
Gọi P là trung điểm MN. Suy ra \(2\overrightarrow{p}=\overrightarrow{m}.\overrightarrow{n}\). Bởi vậy, với \(b=OB,c=OC\) và \(t=\cos<\left(\overrightarrow{u}\overrightarrow{v}\right)\) thì b, c, t là các hằng số và :
\(\overrightarrow{p}=\left[\alpha.\overrightarrow{b}\overrightarrow{u}+\left(1-\alpha\right).\overrightarrow{c}.\overrightarrow{u}\right].\overrightarrow{u}+\left[\alpha.\overrightarrow{b}\overrightarrow{v}+\left(1-\alpha\right).\overrightarrow{c}.\overrightarrow{v}\right].\overrightarrow{v}\)
\(=\alpha.b\left(\overrightarrow{u}+t\overrightarrow{v}\right)+\left(1-\alpha\right).c\left(t\overrightarrow{u}+\overrightarrow{v}\right)\)
\(=\alpha\overrightarrow{x}+\left(1-\alpha\right)\overrightarrow{y}\)
Trong đó \(\overrightarrow{x}=\overrightarrow{OX}=b\left(\overrightarrow{u}+t\overrightarrow{v}\right)\) và \(\overrightarrow{y}=\overrightarrow{OY}=c\left(t\overrightarrow{u}+\overrightarrow{v}\right)\) là các vec tơ cố định
Suy ra P luôn nằm trên đường thẳng XY cố định khi \(\omega\) thay đổi
TOÁN 6 :
O x x' z y 100* 50*
a) \(\widehat{xOz}=\widehat{xOy}+\widehat{yOz}\)
\(100^O=50^O+\widehat{yOz}\)
\(\widehat{yOz}=100^o-50^o\)
\(\widehat{yOz}=50^o\)
b) Vì \(\widehat{xOy}=\widehat{yOz}=\dfrac{\widehat{xOz}}{2}=\dfrac{100^o}{2}=50^o\)
c) Vì Ox' là tia đối của Ox nên suy ra \(\widehat{xOx'}=180^o\)
\(\widehat{xOx'}=\widehat{xOz}+\widehat{zOx'}\)
\(180^o=100^o+\widehat{zOx'}\)
\(\widehat{zOx'}=180^o-100^o\)
\(\widehat{zOx'}=80^o\)
Ta có: A' = (1;2), B' = ( 3;-1)
Đường thằng A'B' có phương trình =
hay 3x + 2y - 7 = 0
Ta có: A' = (1;2), B' = ( 3;-1)
Đường thằng A'B' có phương trình =
hay 3x + 2y - 7 = 0
Gọi A' và d' theo thứ tự là ảnh của A và d qua phép biến hình trên
a) A' = (-1+2; 2+1) = (1;3), d // d', nên d có phương trình : 3x +y + C = 0. Vì A thuộc d, nên A' thuộc d', do đó 3.1 +3 + C = 0. Suy ra C=-6. Do đó phương trình của d' là 3x+y-6=0
b) A (-1;2) và B(0;-1) thuộc d. Ảnh của A và B qua phép đối xứng qua trục Oy tương ứng là A'(1;2) và B'(0;-1). Vậy d' là đường thẳng A'B' có phương trình :
=
hay 3x - y - 1 =0
c) A'=( 1;-2) , d' có phương trình 3x + y -1 =0
d) Qua phép quay tâm O góc , A biến thành A'( -2; -1), B biến thành B'(1;0). Vậy d' là đường thẳng A'B' có phương trình
=
hay x - 3y + 1 = 0
Gọi A' và d' theo thứ tự là ảnh của A và d qua phép biến hình trên
a) A' = (-1+2; 2+1) = (1;3), d // d', nên d có phương trình : 3x +y + C = 0. Vì A thuộc d, nên A' thuộc d', do đó 3.1 +3 + C = 0. Suy ra C=-6. Do đó phương trình của d' là 3x+y-6=0
b) A (-1;2) và B(0;-1) thuộc d. Ảnh của A và B qua phép đối xứng qua trục Oy tương ứng là A'(1;2) và B'(0;-1). Vậy d' là đường thẳng A'B' có phương trình :
=
hay 3x - y - 1 =0
c) A'=( 1;-2) , d' có phương trình 3x + y -1 =0
d) Qua phép quay tâm O góc , A biến thành A'( -2; -1), B biến thành B'(1;0). Vậy d' là đường thẳng A'B' có phương trình
=
hay x - 3y + 1 = 0
Chọn B
· Bổ đề: Trong mặt phẳng cho hai tia Ox và Oy vuông góc với nhau tại gốc O. Trên tia Ox lấy 10 điểm A 1 , A 2 , . . . , A 10 và trên tia Oy lấy 10 điểm B 1 , B 2 , . . . . , B 10 thỏa mãn O A 1 = A 1 A 2 = . . . = A 9 A 10 = O B 1 = B 1 B 2 = . . . . = B 9 B 10 = 1 (đvd).
Tìm số tam giác có 2 đỉnh nằm trong 10 điểm
1 đỉnh nằm trong 10 điểm
B
1
,
B
2
,
.
.
.
.
,
B
10
sao cho tam giác chọn được có đường tròn ngoại tiếp, tiếp xúc với một trong hai trục Ox hoặc Oy?
Giải: Gọi
là 3 đỉnh của tam giác thỏa yêu cầu bài toán với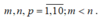 
Ta có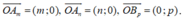
Do đường tròn luôn cắt Ox tại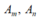
phân biệt nên đường tròn chỉ có thể tiếp xúc với Oy tại
B
p
ta có phương tích
Do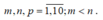
nên dễ thấy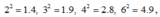 
hay nói cách khác bộ ba (m,n,p)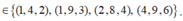
Vậy có 4 tam giác thỏa mãn yêu cầu bổ đề.
· Bài toán: Không gian mẫu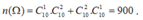
Gọi A là biến cố chọn được tam giác có đường tròn ngoại tiếp tiếp xúc với một trong hai trục Ox hoặc Oy. Theo bổ đề ta chọn được 4 tam giác có 2 đỉnh thuộc tia Ox, 1 đỉnh thuộc tia Oy; tương tự có 4 tam giác có 1 đỉnh thuộc tia Oy, đỉnh thuộc tia . Suy ra, n(A) = 8
Xác suất biến cố A là