Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì ∆ đi qua điểm A song song với (P) => ∆ nằm trong mặt phẳng α với α là mặt phẳng qua
A và song song với P. Suy ra ![]()
Gọi H, K lần lượt là hình chiếu vuông góc của M, N trên
α
. Suy ra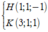
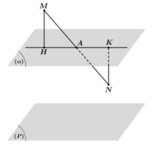
Ta có 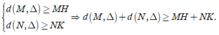
Dấu "=" xảy ra ![]()
Khi đó đường thẳng
∆
có một VTCP là ![]() Đối chiếu các đáp án,
Đối chiếu các đáp án,
chọn B.

Kiểm tra ta thấy d cắt (P)
Đường thẳng cần tìm là giao tuyến của mặt phẳng α với mặt phẳng (P)
Trong đó mặt phẳng α đi qua điểm A và vuông góc với đường thẳng AH, điểm H là hình chiếu của A trên đường thẳng d
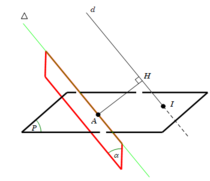
Ta tìm được tọa độ điểm H(-1;0;2) => phương trình mp
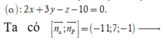 đường thẳng
∆
có một VTVP là
đường thẳng
∆
có một VTVP là
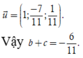
Chọn A.


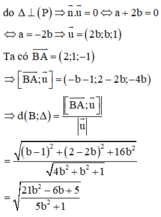

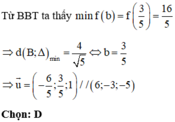
Chú ý khi giải: Các em có thể tham khảo cách 2:
+) Lập phương trình mặt phẳng (Q) đi qua A và song song với (P).
+) Khi đó Δ cần tìm là một đường thẳng nằm trong (Q) và đi qua A.


Đường thẳng d đi qua M ( 0;-1;1 ) và có vectơ chỉ phương là u → 1 ; 2 ; 0 . Do d ⊂ P nên u → . n → = 0 ⇔ a + 2b = 0 nên a = -2b
Đáp án D

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm


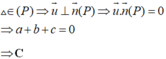
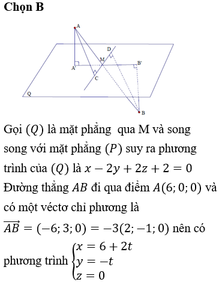

Chọn đáp án B