Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

Đáp án A.
Ta có A M ⊥ B C ⊥ O A ⇒ B C ⊥ O A M ⇒ B C ⊥ O M
Tương tự ta cũng có O M ⊥ A C ⇒ O M ⊥ P ⇒ P (P) nhận O M ¯ = 3 ; 2 ; 1 là vecto pháp tuyến.
Trong các đáp án, chọn đáp án mặt phẳng có vecto pháp tuyến có cùng giá với O M ¯ và không chứa điểm M thì thỏa.

Đáp án C.
Gọi I x ; y ; z thỏa mãn
I A → + 2 I B → + 5 I C → = 0 ⇒ x = 3 + 2. ( − 3 ) + 5. ( − 1 ) 8 = − 1 y = − 1 + 2.0 + 5. ( − 3 ) 8 = − 2 z = − 3 + 2. ( − 1 ) + 5.1 8 = 0
⇒ I = ( − 1 ; − 2 ; 0 )
Ta có
M A → + 2 M B → + 5 M C → = M I → + I A → + 2 M I → + 2 I B → + 5 M I → + 5 I C →
= 8 M I → + I A → + 2 I B → + 5 I C → = 8 M I →
⇒ M A → + 2 M B → + 5 M C → min ⇔ 8 M I → min <=> M là hình chiếu của I lên (P)
Gọi Δ là đường thẳng đi qua I − 1 ; 2 ; 0 và vuông góc với
( P ) : 2 x + 4 y + 3 z − 19 = 0 có vectơ chỉ phương là 2 ; 4 ; 3 ⇒ Δ : x = − 1 + 2 t y = − 2 + 4 t z = 3 t
Thế vào (P)
⇒ 2 ( − 1 + 2 t ) + 4 ( − 2 + 4 t ) + 3 ( 3 t ) − 19 ⇔ t = 1
⇒ x = 1 y = 2 z = 3 ⇒ M 1 ; 2 ; 3 ⇒ a + b + c = 6

Chọn B
Đặt M(x;y;z). Lập hệ 3 phương trình ba ẩn x,y,z từ phương trình mặt phẳng (P) và điều kiện MA=MB, MA=MC

Lời giải:
\(A=a_1a_2+a_2a_3+....+a_{n-1}a_n+a_na_1=0\)
Nếu $n$ lẻ, ta thấy tổng $A$ gồm lẻ số hạng, mỗi số hạng có giá trị $1$ hoặc $-1$ nên $A$ lẻ \(\Rightarrow A\neq 0\) (vô lý)
Do đó $n$ chẵn. Nếu $n$ có dạng $4k+2$. Vì $A=0$ nên trong $4k+2$ số hạng trên sẽ có $2k+1$ số có giá trị là $1$ và $2k+1$ số có giá trị $-1$. Vì mỗi số $a_i$ trong $A$ xuất hiện $2$ lần nên \(a_1a_2a_2a_3....a_{n-1}a_na_{n}a_{1}=(a_1a_2...a_n)^2=1^{2k+1}(-1)^{2k+1}=-1\) (vô lý)
Do đó $n$ phải có dạng $4k$, tức là $n$ chia hết cho $4$ (đpcm)



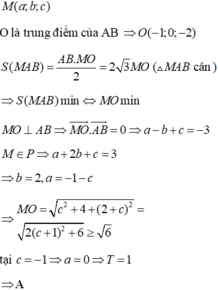
Đáp án là B