Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp:
Tính khoảng cách từ 1 điểm M đến đường thẳng
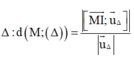
![]()
là 1 điểm bất kì
Cách giải:
![]()
là một VTCP
![]()
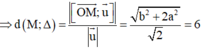
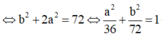
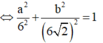
Như vậy tập hợp các điểm M là elip có phương trình
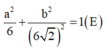
![]()

Câu 1:
S A B C D H M
Lời khuyên là nếu học lớp 12 thì tốt nhất là tọa độ hóa.
Gọi H là trung điểm AB \(\Rightarrow SH\perp\left(ABCD\right)\)
\(CH=\sqrt{BH^2+BC^2}=\sqrt{\left(\frac{AB}{2}\right)^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow SH=CH.tan60^0=a\sqrt{6}\)
Đặt hệ trục tọa độ Oxyz vào hình chóp, tâm O trùng H, Ox trùng toa OB, Oy trùng tia HM với M là trung điểm CD, Oz trùng tia HS, a bằng 1 đơn vị độ dài
Ta được các tọa độ: \(S\left(0;0;\sqrt{6}\right);B\left(1;0;0\right);A\left(-1;0;0\right);C\left(1;1;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{SB}=\left(1;0;-\sqrt{6}\right)\\\overrightarrow{AC}=\left(2;1;0\right)\end{matrix}\right.\) \(\Rightarrow cos\left(SB;AC\right)=\frac{\left|\overrightarrow{SB}.\overrightarrow{AC}\right|}{\left|\overrightarrow{SB}\right|.\left|\overrightarrow{AC}\right|}=\frac{2\sqrt{35}}{35}\)
Câu 2:
\(\overrightarrow{u_{\Delta}}=\overrightarrow{OI}=\left(0;1;1\right)\) ; \(\overrightarrow{n_{Oxy}}=\left(0;0;1\right)\)
Gọi \(\alpha\) là góc tạo bởi \(\Delta\) và Oxy thì \(sin\alpha=\frac{\left|\overrightarrow{u_{\Delta}}.\overrightarrow{n_{Oxy}}\right|}{\left|\overrightarrow{u_{\Delta}}\right|.\left|\overrightarrow{n_{Oxy}}\right|}=\frac{\sqrt{2}}{2}\)
Tới đây, nếu ta đặt tọa độ và tính toán thì rất dài và khó, nhưng sử dụng kiến thức hình học không gian để đơn giản hóa bài toán thì nó sẽ rất dễ.
Trong không gian, tập hợp các điểm cách đều một đường thẳng d cho trước 1 khoảng không đổi \(r\) là hình trụ nhận đường thẳng d làm trục và có bán kính \(r\)
\(\Rightarrow\) Tập hợp các điểm nằm trên Oxy cách đều \(\Delta\) chính là thiết diện cắt bởi hình trụ và mặt phẳng Oxy, đó là 1 hình elip có bán kính trục nhỏ \(a=r=6\) và bán kính trục lớn b được xác định như hình vẽ:
delta mp Oxy r=6 b
\(\Rightarrow b=\frac{r}{sin\alpha}=\frac{6}{\frac{\sqrt{2}}{2}}=6\sqrt{2}\)
Diện tích hình phẳng: \(S=\pi ab=36\pi\sqrt{2}\)

19.
Phương trình mặt phẳng theo đoạn chắn:
\(\frac{x}{3}+\frac{y}{-4}+\frac{z}{-2}=1\)
\(\Leftrightarrow4x-3y-6z-12=0\)
20.
Phương trình mặt phẳng (ABC) theo đoạn chắn:
\(\frac{x}{1}+\frac{y}{2}+\frac{z}{3}=1\)
\(\Leftrightarrow6x+3y+2z-6=0\)
Chẳng đáp án nào đúng cả, chắc bạn ghi nhầm đáp án C số 1 thành số 0 :)
15.
\(2\left(x-2\right)-5\left(y+3\right)+1\left(z+2\right)=0\)
16.
\(\overrightarrow{n_1}=\left(1;1;-1\right)\) ; \(\overrightarrow{n_2}=\left(1;-1;1\right)\)
\(\left[\overrightarrow{n_1};\overrightarrow{n_2}\right]=\left(0;-2;-2\right)=-2\left(0;1;1\right)\)
Phương trình (P):
\(1\left(y-1\right)+1\left(z-1\right)=0\Leftrightarrow y+z-2=0\)
17.
\(\overrightarrow{n_P}=\left(1;-1;1\right)\) ; \(\overrightarrow{n_Q}=\left(3;2;-12\right)\)
\(\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=\left(10;15;5\right)=5\left(2;3;1\right)\)
Phương trình mặt phẳng (R):
\(2x+3y+z=0\)
18.
\(\overrightarrow{MN}=\left(0;-2;3\right);\overrightarrow{MP}=\left(-2;1;3\right)\)
\(\left[\overrightarrow{MN};\overrightarrow{MP}\right]=\left(-9;-6;-4\right)=-1\left(9;6;4\right)\)
Phương trình:
\(9\left(x-2\right)+6\left(y-2\right)+4z=0\)
\(\Leftrightarrow9x+6y+4z-30=0\)

z C B O A D y S x M N
a. Do ABCD là hình thoi có tâm là O nên từ giả thiết ta có :
\(C=\left(-2;0;0\right)\)
\(D=\left(0;-1;0\right)\)
Từ đó M là trung điểm của SC nên :
\(M\left(-1;0=-\sqrt{2}\right)\)
Ta có \(\overrightarrow{SA}=\left(2;0;-2\sqrt{2}\right)\)
\(\overrightarrow{BM}=\left(-1;-1;\sqrt{2}\right)\)
Gọi \(\alpha\) là góc giữa 2 đường thẳng SA, MB, ta có :
\(\cos\alpha=\frac{\left|\overrightarrow{SA.}\overrightarrow{BM}\right|}{\left|\overrightarrow{SA}\right|.\left|\overrightarrow{MB}\right|}=\frac{\left|-2-4\right|}{\sqrt{4+8}.\sqrt{1+2+1}}=\frac{6}{4\sqrt{3}}=\frac{\sqrt{3}}{2}\)
Vậy \(\alpha=60^0\)
Để tính khoảng cách giữa 2 đường thẳng chéo nhau SA, BM ta sử dụng công thức :
\(d\left(SA;BM\right)=\frac{\left|\left[\overrightarrow{SA};\overrightarrow{BM}\right].\overrightarrow{AB}\right|}{\left|\left[\overrightarrow{SA};\overrightarrow{BM}\right]\right|}\) (1)
Theo công thức xác định tọa độ vecto \(\left[\overrightarrow{SA};\overrightarrow{BM}\right]\) ta có :
\(\left[\overrightarrow{SA};\overrightarrow{BM}\right]=\left(\left|\begin{matrix}0&-2\sqrt{2}\\-1&\sqrt{2}\end{matrix}\right|;\left|\begin{matrix}-2\sqrt{2}&2\\\sqrt{2}&-1\end{matrix}\right|;\left|\begin{matrix}2&0\\-1&-1\end{matrix}\right|\right)\)
\(=\left(-2\sqrt{2};1;0\right)\)
\(\Rightarrow\left|\left[\overrightarrow{SA};\overrightarrow{BM}\right]\right|=\sqrt{12}\)
\(\overrightarrow{AB}=\left(-2;1;0\right)\)
\(\Rightarrow\left[\overrightarrow{SA};\overrightarrow{BM}\right].\overrightarrow{AB}=4\sqrt{2}\)
Thay vào (1) ta có :
\(d\left(SA;BM\right)=\frac{4\sqrt{2}}{\sqrt{12}}=\frac{2\sqrt{6}}{3}\)
b. Vì AB \\ mặt phẳng (SDC) nên MN \\ DC. Suy ra N là trung điểm của SD
\(\Rightarrow N=\left(0;-\frac{1}{2};\sqrt{2}\right)\)
Dễ thấy :
\(V_{S.ABMN}=V_{S.ABN}+V_{S.BMN}\)
\(=\frac{1}{6}\left|\left[\overrightarrow{SA};\overrightarrow{BM}\right].\overrightarrow{SN}\right|+\frac{1}{6}\left|\left[\overrightarrow{SB};\overrightarrow{SM}\right].\overrightarrow{SN}\right|\) (2)
Ta có \(\overrightarrow{SA}=\left(2;0;-2\sqrt{2}\right)\)
\(\overrightarrow{SN}=\left(0;-\frac{1}{2};-\sqrt{2}\right)\)
\(\overrightarrow{SB}=\left(0;1;-2\sqrt{2}\right)\)
\(\overrightarrow{SM}=\left(-1;0;-\sqrt{2}\right)\)
Ta lại có :
\(\left[\overrightarrow{SA};\overrightarrow{SB}\right]=\left(\left|\begin{matrix}0&-2\sqrt{2}\\-1&-2\sqrt{2}\end{matrix}\right|;\left|\begin{matrix}-2\sqrt{2}&2\\-2\sqrt{2}&0\end{matrix}\right|;\left|\begin{matrix}2&0\\0&1\end{matrix}\right|\right)\)
\(=\left(2\sqrt{2};4\sqrt{2};2\right)\)
\(\left[\overrightarrow{SB};\overrightarrow{SM}\right]=\left(\left|\begin{matrix}1&-2\sqrt{2}\\0&\sqrt{2}\end{matrix}\right|;\left|\begin{matrix}-2\sqrt{2}&0\\-\sqrt{2}&-1\end{matrix}\right|;\left|\begin{matrix}0&1\\-1&0\end{matrix}\right|\right)\)
\(=\left(-\sqrt{2};2\sqrt{2};1\right)\)
Thay vào (2) được :
\(V_{S.ABMN}=\frac{1}{6}\left(\left|-2\sqrt{2}-2\sqrt{2}\right|+\left|-\sqrt{2}-\sqrt{2}\right|\right)=\sqrt{2}\)

Câu 28:
\(\overrightarrow{CB}=\left(1;-1;1\right)\)
Do (P) vuông góc BC nên nhận (1;-1;1) là 1 vtpt
Phương trình (P):
\(1\left(x-1\right)-1\left(y-1\right)+1\left(z+5\right)=0\)
\(\Leftrightarrow x-y+z+5=0\)
Câu 29:
Mạt phẳng (Q) nhận \(\left(1;-2;3\right)\) là 1 vtpt nên nhận các vecto có dạng \(\left(k;-2k;3k\right)\) cũng là các vtpt với \(k\ne0\)
Do đó đáp án B đúng (ko tồn tại k thỏa mãn)
Với đáp án A thì \(k=-2\) , đáp án C thì \(k=3\), đáp án D có \(k=1\)

B C A D H K J S
Kẻ \(SH\perp AC\left(H\in AC\right)\)
Do \(\left(SAC\right)\perp\left(ABCD\right)\Rightarrow SH\perp\left(ABCD\right)\)
\(SA=\sqrt{AC^2-SC^2}=a;SH=\frac{SA.SC}{AC}=\frac{a\sqrt{3}}{2}\)
\(S_{ABCD}=\frac{AC.BD}{2}=2a^2\)
\(V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}=\frac{1}{3}.\frac{a\sqrt{3}}{2}.2a^2=\frac{a^3\sqrt{3}}{3}\)
Ta có \(AH=\sqrt{SA^2-SH^2}=\frac{a}{2}\Rightarrow CA=4HA\Rightarrow d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Do BC//\(\left(SAD\right)\Rightarrow d\left(B,\left(SAD\right)\right)=d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Kẻ \(HK\perp AD\left(K\in AD\right),HJ\perp SK\left(J\in SK\right)\)
Chứng minh được \(\left(SHK\right)\perp\left(SAD\right)\) mà \(HJ\perp SK\Rightarrow HJ\perp\left(SAD\right)\Rightarrow d\left(H,\left(SAD\right)\right)=HJ\)
Tam giác AHK vuông cân tại K\(\Rightarrow HK=AH\sin45^0=\frac{a\sqrt{2}}{4}\)
\(\Rightarrow HJ=\frac{SH.HK}{\sqrt{SH^2+HK^2}}=\frac{a\sqrt{3}}{2\sqrt{7}}\)
Vậy \(d\left(B,\left(SAD\right)\right)=\frac{2a\sqrt{3}}{\sqrt{7}}=\frac{2a\sqrt{21}}{7}\)

14.
Mặt phẳng (P) nhận \(\overrightarrow{n}=\left(2;1;-2\right)\) là 1 vtpt
Đường thẳng d nhận \(\overrightarrow{u}=\left(1;-2;3\right)\) là 1 vtcp
Điểm \(M\left(2;0;-3\right)\) thuộc d nên cũng thuộc (Q)
(Q) vuông góc (P) và chứa d nên nhận \(\left[\overrightarrow{n};\overrightarrow{u}\right]=\left(1;8;5\right)\) là 1 vtpt
Phương trình (Q):
\(1\left(x-2\right)+8y+5\left(z+3\right)=0\)
\(\Leftrightarrow x+8y+5z+13=0\)
15.
Phương trình hoành độ giao điểm:
\(sinx=cosx\Rightarrow x=\frac{\pi}{4}\)
\(S=\int\limits^{\frac{\pi}{4}}_0\left(cosx-sinx\right)dx+\int\limits^{\pi}_{\frac{\pi}{4}}\left(sinx-cosx\right)dx=\sqrt{2}-1+\sqrt{2}+1=2\sqrt{2}\)
10.
Coi lại đề nào bạn, pt hình phẳng (D) có vấn đề, nhìn chữ -dx+4 kia ko biết phải nghĩ sao
11.
Cũng ko dịch được đề này, đoán đại: cho \(F\left(x\right)=x^2\) là 1 nguyên hàm của \(f\left(x\right).e^{2x}\). Tìm nguyên hàm của \(f'\left(x\right).e^{2x}\)
\(I=\int f'\left(x\right)e^{2x}dx\)
Đặt \(\left\{{}\begin{matrix}u=e^{2x}\\dv=f'\left(x\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2e^{2x}dx\\v=f\left(x\right)\end{matrix}\right.\)
\(\Rightarrow I=e^{2x}f\left(x\right)-2\int f\left(x\right)e^{2x}dx=e^{2x}f\left(x\right)-2x^2+C\)
12.
Đúng là \(y=\left(e+1\right)x\) và \(y=1+e^x\) chứ bạn? Hai đồ thị này cắt nhau tại 2 điểm, nhưng ko thể tìm được tọa độ của điểm thứ 2 đâu
13.
Hình chiếu của A lên Ox có tọa độ \(\left(1;0;0\right)\)

Vậy quỹ tích M trên (Oxy) là hình Elip với