Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
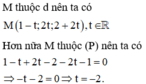
Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

Chọn A.
Phương pháp: Điều kiện để đường thẳng vuông góc với mặt phẳng là véc tơ chỉ phương của đường thẳng và véc tơ pháp tuyến của mặt phẳng cùng phương.


Đáp án C.
Ta có B C → = - 2 ; - 1 ; - 2 nên phương trình đường thẳng BC là x = 1 - 2 t y = - t ( t ∈ ℝ ) z = 2 - 2 t .
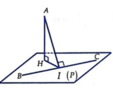
Gọi I là hình chiếu vuông góc của A trên BC, H là hình chiếu vuông góc của A trên mặt phẳng (P) . Khi đó A H = d A ; P ≤ A I và AH đạt giá trị lớn nhất khi H ≡ I . Suy ra mặt phẳng (P) qua I và vuông góc với AI.
Từ I ∈ B C ⇒ I 1 - 2 t ; - t ; 2 - 2 t và A I → = - 1 - 2 t ; - t - 5 ; - 1 - 2 t .
Lại có A I ⊥ B C ⇔ A I → . B C → = 0 ⇔ 2 ( 1 + 2 t ) + ( t + 5 ) + 2 ( 1 + 2 t ) = 0 ⇔ t = - 1 .
Mặt phẳng (P) đi qua I(3;1;4) và nhận VTPT là A I → = 1 ; - 4 ; 1 nên có phương trình tổng quát là: x - 4 y + z - 3 = 0 .
Vậy a = 1 , b = - 4 , c = 1 , d = - 3 → M = 1 + 1 - 4 - 3 = - 2 7 .

Mặt cầu (S) có tâm I(0;1;1) và bán kính R = 3
Ta có 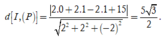
Vậy khoảng cách ngắn nhất: ![]()
Chọn A.
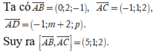


Chọn đáp án C
Ta có A B ⇀ = 0 ; 2 ; - 1 , A C ⇀ = - 1 ; 1 ; 2 và A D ⇀ = - 1 ; m + 2 ; p .
Suy ra A B ⇀ , A C ⇀ = 5 ; 1 ; 2
⇒ A B ⇀ , A C ⇀ . A D ⇀ = m + 2 p - 3
Để bốn điểm A, B, C, D đồng phẳng thì A B ⇀ , A C ⇀ . A D ⇀
⇔ m + 2 p = 3