Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường thẳng a: 3x - 4y - 31 = 0
Gọi I ( x; y ) là tâm của đương tròn cần tìm
Ta có: d( I; a ) = IA = 5 =>\(\frac{\left|3x-4y-31\right|}{\sqrt{3^2+4^2}}=5\) <=> \(\left|3x-4y-31\right|=25\)<=> 3x - 4y - 31 = 25 ( 1) hoặc 3x - 4y - 31 = -25 ( 2)
a có VTPT \(\overrightarrow{n}\) = ( 3; -4) => a có VTCP \(\overrightarrow{u}\) = ( 4; 3 )
Lại có: IA vuông góc với a => ( 1- x ) . 4 + 3 ( - 7 - y ) = 0 <=> - 4x -3 y = 17 (3)
Từ (1) ; (3) => \(I_1\left(4;-11\right)\)
Từ (2) ; (3) => \(I_2\left(-2;-3\right)\)
Đáp án A

Gọi I là tâm của đường tròn cần tìm
Vì I thuộc d1 : 3x - y - 5 = 0 và có tung độ âm => I ( x; 3x - 5 ) với 3x - 5 < 0
Gọi A; B là giao điểm của d2 : x - 4 = 0 với đường tròn
=> AB = 8
Gọi M là trung điểm của AB => AM = 8: 2 = 4
=> d( I ; d2 ) = IM = \(\sqrt{AI^2-AM^2}=\sqrt{5^2-4^2}=3\)
khi đó ta có: \(\frac{\left|x-4\right|}{1}=3\)
<=> \(\orbr{\begin{cases}x-4=3\\x-4=-3\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=7\\x=1\end{cases}}\)
Với x = 7 => I ( 7; 16 ) loại vì 16 > 0
Với x = 1 => I ( 1; -2)
Phương trình đường tròn cần tìm là: ( x - 1 )^2 + ( y + 2 ) ^2 = 25
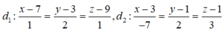

Đáp án B
Ta có d 1 đi qua điểm M 1 (7; 3; 9) và có vectơ chỉ phương là u 1 → = (1; 2; 1); d 2 đi qua điểm M 2 (3; 1; 1) và có vectơ chỉ phương là u 2 → .