Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O u 3 a t M 2a
Điều kiện sóng dừng 2 đầu cố định: \(l=\frac{k\lambda}{2}\Rightarrow\lambda=l=\frac{v}{f}\Rightarrow f=\frac{v}{l}\)(Với k = 2, vì trên hình có 2 bụng).
Thời gian từ \(u=x\rightarrow u=-x\) (liên tiếp): \(5\Delta t-\Delta t=4\Delta t\)
Suy ra thời gian từ vị trí: \(u=x\rightarrow u=0\) là: \(\frac{4\Delta t}{2}=2\Delta t\)
Suy ra thời gian đi từ vị trí: \(u=2a\rightarrow u=0\) (biên về VTCB) là \(\Delta t+2\Delta t=3\Delta t=\frac{T}{4}\)
Chu kì dao động: \(T=4.3\Delta t=12\Delta t\)
Suy ra: \(A_M=x=2a.\frac{\sqrt{3}}{2}=a\sqrt{3}\) (dựa vào hình vẽ, cung \(\Delta t\) ứng với 300).
Dựa vào vòng tròn: \(V_M\) \(_{max}=a\sqrt{3}.\omega=a\sqrt{3}.2\pi f=2\pi\sqrt{3}\frac{va}{l}\)
Đáp án B

Hướng dẫn:
\(U_{AB}=U_C=2\) (1)
\(U_{BC}^2=U_r^2+U_L^2=3\) (2)
\(U_{AC}^2=U_r^2+(U_L-U_C)^2=1\) (3)
Giải hệ 3 pt trên sẽ tìm đc \(U_r\) và \(U_L\)
Chia cho \(I\) sẽ tìm được \(r\) và \(Z_L\)

Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\)
\(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**)
Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\)
A đúng

Mạch chỉ có điện trở thuần thì u cùng pha với i.
Nếu \(u=U_0\cos\left(\omega t+\varphi\right)\)
Thì: \(i=I_0\cos\left(\omega t+\varphi\right)\)
\(\Rightarrow\frac{u}{U_0}=\frac{i}{I_0}\)
\(\Rightarrow\frac{u^2}{U_0^2}+\frac{i^2}{I_0^2}=1\) là sai.

Từ ĐK đầu bài ta có:
tần số dao động riwwng của mạch là:
giải phương trình bâc 2 này ra ta được:

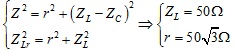
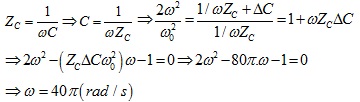
Chọn đáp án A