Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giải thích: Đáp án D
Phương pháp: Hệ số công suất cosφ = R/Z
Cách giải:
Ta có: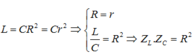 
Có: 
Thay ZL = 3ZC vào biểu thức L.ZC = R2 ta được:
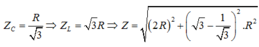
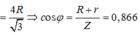
Chuẩn hóa R = r = 1 ⇒ Z L = X Z C = 1 X
Ta có U R C = 3 U d ⇔ 1 2 + 1 X 2 = 3 1 + X 2 ⇒ X = 0 , 528
Hệ số công suất của mạch cos φ = 2 1 2 + X − 1 X 2 ≈ 0 , 83
Đáp án A
Đáp án B
Phương pháp: Sử dụng công thức tính công suất và giản đồ vecto
Cách giải:
Ta có 
Khi
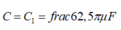thì
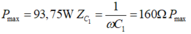
khi I max có xảy ra cộng hưởng
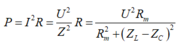
Thay số từ đề bài P = 93,75W; U = 150; ta tính được Rm = 240Ω
thì U d vuông pha với U RC cho ta biết cuộn dây có điện trở trong r.
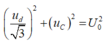
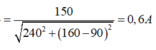
Vì ULr vuông góc với URC nên:
Mặt khác theo định luật Ôm ta có:
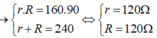
Đáp án C
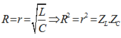
Đặt ZL = 1 và ZC = x => R2 = r2 = x
Vì theo đề bài: UMB = n.UAM => ZMB = nZAM
Hệ số công suất của mạch: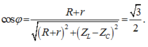 
Đáp án B
+ Ta có 
(mạch xảy ra cộng hưởng) => công suất tiêu thụ của mạch là cực đại.
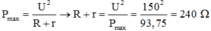
+ Khi 
, điện áp hai đầu cuộn dây vuông pha với điện áp hai đầu đoạn mạch RC
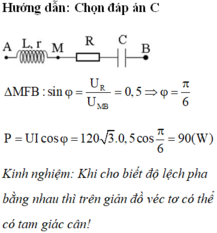
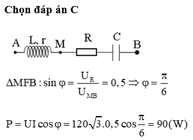
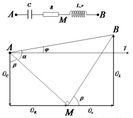
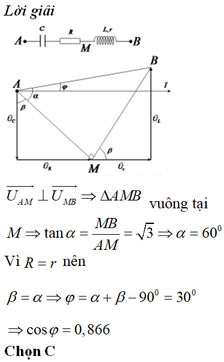
Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\)
\(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**)
Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\)
A đúng
Ta có: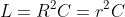
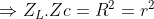
Điện áp hiệu dụng của đoạn mạch RC gấp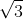
lần điện áp hiệu dụng hai đầu cuộn dây
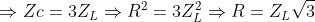
=> Hệ số công suất của đoạn mạch là