Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

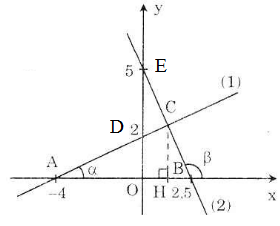
a) * Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0, tính được y = 2 => D(0; 2) thuộc đồ thị.
Cho y = 0, 0 = 0,5.x + 2 => x = -4 => A(-4; 0) thuộc đồ thị. Đường thẳng vẽ qua A, D là đồ thị của (1).
*Vẽ đồ thị hàm số y = 5 – 2x (2)
-Cho x = 0 tính được y = 5 E(0; 5) thuộc đồ thị
-Cho y = 0, 0 = 5 – 2x => x = 2,5 => B(2,5; 0) thuộc đồ thị. Đường thẳng vẽ qua B, E là đồ thị của (2).
b) Ở câu a) ta tính được tọa độ của hai điểm A và B: A(-4; 0), B(2,5; 0)

Hoành độ giao điểm của (d) và (P) là nghiệm của pt
\(kx+\frac{1}{2}=\frac{1}{2}x^2\)
\(\Leftrightarrow x^2-2kx-1=0\left(1\right)\)
Để (d) cắt (P) tại 2 điểm phân biệt thì pt (1) phải có 2 nghiệm phân biệt
Khi đó: \(\Delta'>0\)
\(\Leftrightarrow k^2+1>0\)(Luôn đúng)
Theo Vi-ét ta có: xA + xB = 2k
xA . xB = -1
Vì \(A;B\in\left(P\right)\)
\(\Rightarrow\hept{\begin{cases}y_A=\frac{1}{2}x_A^2\\y_B=\frac{1}{2}x_B^2\end{cases}}\)
Gọi I(xI ; yI) là trung điểm AB
Khi đó: \(x_I=\frac{x_A+x_B}{2}=\frac{2k}{2}=k\)
\(y_I=\frac{y_A+y_B}{2}=\frac{x^2_A+x_B^2}{4}=\frac{\left(x_A+x_B\right)^2-2x_Ax_B}{4}=\frac{4k^2+2}{4}=k^2+\frac{1}{2}\)
Do đó: \(y_I=x_I^2+\frac{1}{2}\)
Nên I thuộc \(\left(P\right)y=x^2+\frac{1}{2}\)
Vậy ...............
P/S: nếu bạn thắc mắc về \(\left(P\right)=x^2+\frac{1}{2}\)thì mình sẽ giải thích
Ở cấp 2 thì ta chỉ được gặp dạng (P) y = ax2 có đỉnh trùng với gốc tọa độ
Nhưng đây chỉ là dạng đặc biệt của nó thôi . Còn dạng chuẩn là (P) y = ax2 + bx + c . (P) này có đỉnh không trùng với gốc tọa độ

Lời giải
Tổng quát
trong mặt phẳng tọa Oxy Đường thẳng có phương trình
y=a x +b
.........Vấn đề ta phải đi xác định các hệ số : a,b
a)
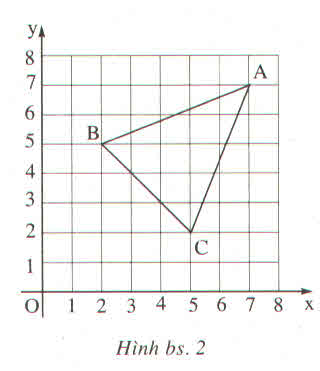
a.1) đi qua A;B
a,b thủa mãn hệ phương trình
\(\left\{{}\begin{matrix}4a+b=5\\a+b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=2\\b=-3\end{matrix}\right.\) \(\Rightarrow\left(AB\right)d_1:y=2x-3\)
a.2) đi Qua BC
a,b thủa mãn hệ phương trình
\(\left\{{}\begin{matrix}4a+b=-4\\a+b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-1\\b=0\end{matrix}\right.\) \(\Rightarrow\left(BC\right)d_2:y=-x\)
a.3) đi qua CD
a,b thủa mãn hệ phương trình
\(\left\{{}\begin{matrix}4a+b=-4\\7a+b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-8\end{matrix}\right.\) \(\Rightarrow\left(CD\right)d_3:y=x-8\)
a.4) đi qua DA
a,b thủa mãn hệ phương trình
\(\left\{{}\begin{matrix}4a+b=5\\7a+b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=13\end{matrix}\right.\)\(\Rightarrow\left(DA\right)d_4:y=-2x-13\)
việc sử dụng máy tính ==> suy ra ra góc --> cái đó quá tầm thường rồi.
Mấu chốt vấn Vấn đề biết ý nghĩa hệ số "a" => ra tất cả
ý nghĩa hệ số a vẫn có vị rất quan trọng trong tọa độ phẳng (tương đương sức f(1) trong phương trình đại số )
nhiều bài toán biết cách vận dụng nó -->bài toán trở lên quá đơn giải --> dẫn đến bất ngờ

Hai đường chéo AC và BD vuông góc với nhau tại I.
- Đường thẳng AB có hệ số góc bằng 2, do đó ta có
tgα = 2 ⇒ α = 63 ° 26 ' (tính trên máy tính bỏ túi).
Suy ra ∠ (ABD) ≈ 63 ° 26 '
Tam giác ABD cân, nên cũng có ∠ (ADB) ≈ 63 ° 26 '
Từ đó suy ra ∠ (BAD) = 180 ° - 2. 63 ° 26 ' ≈ 53 ° 8 '
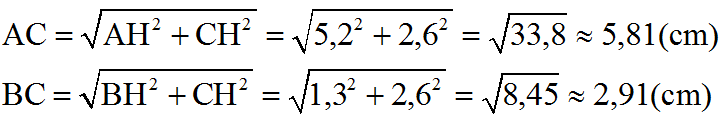



Phương trình của đường thẳng AB có dạng: y = ax + b.
Do phương trình đi qua A(4;5) và B(1; -1) nên ta có:
5 = a.4 + b (1)
-1 = a.1 + b (2)
Trừ từng vế của (1) và (2), ta có: 6 = 3a ⇒ a = 2.
Thay a = 2 và (1) để tìm b, ta có 5 = 2.4 + b ⇒ b = -3.
Vậy phương trình đường thẳng AB là: y = 2x – 3.
Làm tương tự như trên, ta có:
Phương trình đường thẳng BC là: y = -x.
Phương trình đường thẳng CD là: y = x – 8.
Phương trình đường thẳng DA là: y = -2x + 13.