Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Câu 1:
\(cos7x-\sqrt{3}sin7x=-2\\ \Leftrightarrow cos\left(7x+\dfrac{\pi}{3}\right)=-1\\ \Leftrightarrow7x+\dfrac{\pi}{3}=-\pi+k2\pi\\ \Leftrightarrow x=-\dfrac{4\pi}{21}+k\dfrac{2\pi}{7}\)
Vì \(x\in[\dfrac{2\pi}{5};\dfrac{6\pi}{7}]\)
\(\Rightarrow\dfrac{2\pi}{5}\le x\le\dfrac{6\pi}{7}\\ \Leftrightarrow\dfrac{2\pi}{5}\le-\dfrac{4\pi}{21}+k\dfrac{2\pi}{7}\le\dfrac{6\pi}{7}\\ \Leftrightarrow\dfrac{31}{15}\le k\le\dfrac{11}{3}\)
Vì \(k\in Z\) nên \(k=3\)
Vậy \(x\) cần tìm là \(\dfrac{2\pi}{3}\)
Câu 2:
\(2sin^2x-sinxcosx-cos^2x=m\\ \Leftrightarrow2\dfrac{1-cos2x}{2}-\dfrac{1}{2}s\text{in2}x-\dfrac{1+cos2x}{2}=m\\ \Leftrightarrow3cos2x+s\text{in2}x=1-2m\)
Điều kiện để phương trình có nghiệm là:
\(3^2+1^2\ge\left(1-2m\right)^2\\ \Leftrightarrow4m^2-4m-9\le0\\ \Leftrightarrow\dfrac{1-\sqrt{10}}{2}\le m\le\dfrac{1+\sqrt{10}}{2}\)
1/ \(y=x^{-1}+\frac{2}{3}x^{-2}-\frac{2}{3}\Rightarrow y'=-\frac{1}{x^2}-\frac{4}{3x^3}\)
\(3x^3y'+3x+4=3x^3\left(-\frac{1}{x^2}-\frac{4}{3x^3}\right)+3x+4\)
\(=-3x-4+3x+4=0\) (đpcm)
2/ \(y'\le0\)
\(\Leftrightarrow3x^2-10x+7\le0\)
\(\Leftrightarrow1\le x\le\frac{7}{3}\)
a.
\(1-sin^2x+1-2sin^2x+sinx+2=0\)
\(\Leftrightarrow-3sin^2x+sinx+4=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-1\\sinx=\frac{4}{3}\left(l\right)\end{matrix}\right.\)
\(\Rightarrow x=-\frac{\pi}{2}+k2\pi\)
b. ĐKXĐ; ...
\(5tanx-\frac{2}{tanx}-3=0\)
\(\Leftrightarrow5tan^2x-3tanx-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tanx=-\frac{2}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=arctan\left(-\frac{2}{5}\right)+k\pi\end{matrix}\right.\)
e.
Ko rõ vế phải
f.
\(\Leftrightarrow1-3sin^2x.cos^2x=\frac{5}{6}\left(1-2sin^2x.cos^2x\right)\)
\(\Leftrightarrow1-\frac{3}{4}sin^22x=\frac{5}{6}\left(1-\frac{1}{2}sin^22x\right)\)
\(\Leftrightarrow1-2sin^22x=0\)
\(\Leftrightarrow cos4x=0\)
\(\Leftrightarrow x=\frac{\pi}{8}+\frac{k\pi}{4}\)
16.
\(y'=\frac{\left(cos2x\right)'}{2\sqrt{cos2x}}=\frac{-2sin2x}{2\sqrt{cos2x}}=-\frac{sin2x}{\sqrt{cos2x}}\)
17.
\(y'=4x^3-\frac{1}{x^2}-\frac{1}{2\sqrt{x}}\)
18.
\(y'=3x^2-2x\)
\(y'\left(-2\right)=16;y\left(-2\right)=-12\)
Pttt: \(y=16\left(x+2\right)-12\Leftrightarrow y=16x+20\)
19.
\(y'=-\frac{1}{x^2}=-x^{-2}\)
\(y''=2x^{-3}=\frac{2}{x^3}\)
20.
\(\left(cotx\right)'=-\frac{1}{sin^2x}\)
21.
\(y'=1+\frac{4}{x^2}=\frac{x^2+4}{x^2}\)
22.
\(lim\left(3^n\right)=+\infty\)
11.
\(\lim\limits_{x\rightarrow1^+}\frac{-2x+1}{x-1}=\frac{-1}{0}=-\infty\)
12.
\(y=cotx\Rightarrow y'=-\frac{1}{sin^2x}\)
13.
\(y'=2020\left(x^3-2x^2\right)^{2019}.\left(x^3-2x^2\right)'=2020\left(x^3-2x^2\right)^{2019}\left(3x^2-4x\right)\)
14.
\(y'=\frac{\left(4x^2+3x+1\right)'}{2\sqrt{4x^2+3x+1}}=\frac{8x+3}{2\sqrt{4x^2+3x+1}}\)
15.
\(y'=4\left(x-5\right)^3\)
\(cos\left(\frac{x}{2}+15^0\right)=sinx=cos\left(90^0-x\right)\)
\(\Rightarrow\left[{}\begin{matrix}\frac{x}{2}+15^0=90^0-x+k360^0\\\frac{x}{2}+15^0=x-90^0+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=50^0+k240^0\\x=210^0+k720^0\end{matrix}\right.\)
Với \(k=1\Rightarrow x=290^0\)
Bài 2:
\(\Leftrightarrow2sinx+2sinx.cosx-cosx-cos^2x-sin^2x=0\)
\(\Leftrightarrow2sinx+2sinx.cosx-cosx-1=0\)
\(\Leftrightarrow2sinx\left(cosx+1\right)-\left(cosx+1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(cosx+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=\frac{1}{2}\\cosx=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\) đáp án B
3/ \(y=\frac{sinx+cosx-1}{sinx-cosx+3}\)
\(\Leftrightarrow y.sinx-y.cosx+3y=sinx+cosx-1\)
\(\Leftrightarrow\left(y-1\right)sinx-\left(y+1\right)cosx=-3y-1\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(y-1\right)^2+\left(y+1\right)^2\ge\left(-3y-1\right)^2\)
\(\Leftrightarrow7y^2+6y-1\le0\)
\(\Rightarrow-1\le y\le\frac{1}{7}\Rightarrow y_{max}=\frac{1}{7}\)
1) đặc : \(f\left(x\right)=y=cot4x\)
điều kiện xác định : \(sin4x\ne0\Leftrightarrow4x\ne k\pi\Leftrightarrow x\ne\dfrac{k\pi}{4}\)
\(\Rightarrow x\in D\) thì \(-x\in D\)
ta có : \(f\left(-x\right)=cot\left(-4x\right)=-cot4x=-f\left(x\right)\)
\(\Rightarrow\) hàm này là hàm lẽ
2) đặc : \(f\left(x\right)=y=\left|cotx\right|\)
điều kiện xác định : \(sinx\ne0\Leftrightarrow x\ne k\pi\)
\(\Rightarrow x\in D\) thì \(-x\in D\)
ta có : \(f\left(-x\right)=\left|cot\left(-x\right)\right|=\left|-cotx\right|=\left|cotx\right|=f\left(x\right)\)
\(\Rightarrow\) hàm này là hàm chẳn
3) đặc : \(f\left(x\right)=y=1-sin^2x=cos^2x\)
điều kiện xác định : \(D=R\)
\(\Rightarrow x\in D\) thì \(-x\in D\)
ta có : \(f\left(-x\right)=cos^2\left(-x\right)=cos^2x=f\left(x\right)\)
\(\Rightarrow\) hàm này là hàm chẳn
4) đặc : \(f\left(x\right)=y=sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{sinx+cosx}{\sqrt{2}}\)
điều kiện xác định : \(D=R\)
\(\Rightarrow x\in D\) thì \(-x\in D\)
ta có : \(f\left(-x\right)=\dfrac{sin\left(-x\right)+cos\left(-x\right)}{\sqrt{2}}=\dfrac{-sinx+cosx}{\sqrt{2}}\ne f\left(x\right);-f\left(x\right)\)
\(\Rightarrow\) hàm này là hàm không chẳn không lẽ
mấy bài còn lại bn làm tương tự cho quen nha
Ta có : Cy(x+1) : Cy+1(x) = 6:5
<=> 5(x-1)(y+1) = 6(x-y)(x-y+1) (1)
Lại có : Cy(x+1) : Cy-1(x) = 6:2
<=> x+1=3y (2)
Thay (2) vào (1) => 9y^2-27y=0
<=> y=3 hoặc y=0(loại)
=> x=8
Chọn D.
Sử dụng công thức đạo hàm của hàm hợp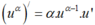
(với u = x7 + x )
y' = 2(x7 + x).(x7 + x)’ = 2(x7 + x)(7x6 + 1)