
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

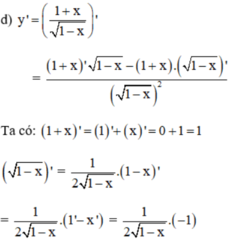
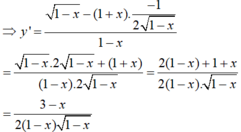

xét hàm số y=ln(\(x+\sqrt{1+x^2}\))
Ta có
y'=\(\frac{1}{x+\sqrt{1+x^2}}\left(1+\frac{x}{\sqrt{1+x^2}}\right)=\frac{1}{x+\sqrt{1+x^2}}.\frac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}}=\frac{1}{\sqrt{1+x^2}}\)

Lời giải:
a) y' = =
, y" =
=
=
.
b) y' = =
;
y" = =
=
.
c) y' = ; y" =
=
=
.
d) y' = 2cosx.(cosx)' = 2cosx.(-sinx) = - 2sinx.cosx = -sin2x,
y" = -(2x)'.cos2x = -2cos2x.

a) Giả sử ∆x là số gia của số đối tại x0= 1. Ta có:
∆y = f(1 + ∆x) - f(1) = 7 + (1 + ∆x) - (1 + ∆x)2 - (7 + 1 - 12) = -(∆x)2 - ∆x ;
= - ∆x - 1 ;
=
(- ∆x - 1) = -1.
Vậy f'(1) = -1.
b) Giả sử ∆x là số gia của số đối tại x0= 2. Ta có:
∆y = f(2 + ∆x) - f(2) = (2 + ∆x)3 - 2(2 + ∆x) + 1 - (23 - 2.2 + 1) = (∆x)3 + 6(∆x)2 + 10∆x;
= (∆x)2 + 6∆x + 10;
=
[(∆x)2 + 6∆x + 10] = 10.
Vậy f'(2) = 10.

a) Giả sử ∆x là số gia của số đối tại x0 = 1. Ta có:
∆y = f(1 + ∆x) - f(1) = (1 + ∆x)2 + (1 + ∆x) - (12+ 1) = 3∆x + (∆x)2;
= 3 + ∆x;
=
(3 + ∆x) = 3.
Vậy f'(1) = 3.
b) Giả sử ∆x là số gia của số đối tại x0 = 2. Ta có:
∆y = f(2 + ∆x) - f(2) = -
= -
;
= -
;
=
-
= -
.
Vậy f'(2) = - .
c) Giả sử ∆x là số gia của số đối tại x0 = 0.Ta có:
∆y = f(∆x) - f(0) = - ( -1) =
;
=
;
=
= -2.
Vậy f'(0) = -2


a. \(y'=\dfrac{-1}{\left(x-1\right)}\)
b. \(y'=\dfrac{5}{\left(1-3x\right)^2}\)
c. \(y=\dfrac{\left(x+1\right)^2+1}{x+1}=x+1+\dfrac{1}{x+1}\Rightarrow y'=1-\dfrac{1}{\left(x+1\right)^2}=\dfrac{x^2+2x}{\left(x+1\right)^2}\)
d. \(y'=\dfrac{4x\left(x^2-2x-3\right)-2x^2\left(2x-2\right)}{\left(x^2-2x-3\right)^2}=\dfrac{-4x^2-12x}{\left(x^2-2x-3\right)^2}\)
e. \(y'=1+\dfrac{2}{\left(x-1\right)^2}=\dfrac{x^2-2x+3}{\left(x-1\right)^2}\)
g. \(y'=\dfrac{\left(4x-4\right)\left(2x+1\right)-2\left(2x^2-4x+5\right)}{\left(2x+1\right)^2}=\dfrac{4x^2+4x-14}{\left(2x+1\right)^2}\)
2.
a. \(y'=4\left(x^2+x+1\right)^3.\left(x^2+x+1\right)'=4\left(x^2+x+1\right)^3\left(2x+1\right)\)
b. \(y'=5\left(1-2x^2\right)^4.\left(1-2x^2\right)'=-20x\left(1-2x^2\right)^4\)
c. \(y'=3\left(\dfrac{2x+1}{x-1}\right)^2.\left(\dfrac{2x+1}{x-1}\right)'=3\left(\dfrac{2x+1}{x-1}\right)^2.\left(\dfrac{-3}{\left(x-1\right)^2}\right)=\dfrac{-9\left(2x+1\right)^2}{\left(x-1\right)^4}\)
d. \(y'=\dfrac{2\left(x+1\right)\left(x-1\right)^3-3\left(x-1\right)^2\left(x+1\right)^2}{\left(x-1\right)^6}=\dfrac{-x^2-6x-5}{\left(x-1\right)^4}\)
e. \(y'=-\dfrac{\left[\left(x^2-2x+5\right)^2\right]'}{\left(x^2-2x+5\right)^4}=-\dfrac{2\left(x^2-2x+5\right)\left(2x-2\right)}{\left(x^2-2x+5\right)^4}=-\dfrac{4\left(x-1\right)}{\left(x^2-2x+5\right)^3}\)
f. \(y'=4\left(3-2x^2\right)^3.\left(3-2x^2\right)'=-16x\left(3-2x^2\right)^3\)