Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có : 2 + 4 + 6 + 8 +... + 16 + 18
SSH : (18 - 2) : 2 + 1 = 9(số)
Tổng : (2 + 18).9 : 2 = 90
\(A=\frac{27\cdot45+27\cdot45}{90}=\frac{27\left(45+45\right)}{90}=\frac{27\cdot90}{90}=27\)
b) Ta có : 135.1420 + 45.780.3 = 135.1420 + 135.780 = 135(1420 + 780) = 135.2200 (*)
3 + 6 + 9 + 12 + ... + 24 + 27
Số số hạng : (27 - 3) : 3 + 1 = 9(số)
Tổng : (3 + 27).9 : 2 = 135 (**)
Từ (*) và (**) suy ra
=> \(B=\frac{135\cdot2200}{135}=2200\)
a)
2 + 4 + 6 + ... + 16 + 18
Số số hạng :
( 18 - 2 ) / 2 + 1 = 9
Tổng :
( 18 + 2 ) x 9 / 2 = 90
\(A=\frac{27\cdot45+27\cdot45}{90}\)
\(=\frac{27\left(45+45\right)}{90}\)
\(=\frac{27\cdot90}{90}\)
\(=27\)
b)
3 + 6 + 9 + 12 + ... + 24 + 27
Số số hạng :
( 27 - 3 ) / 3 + 1 = 9
Tổng :
( 27 + 3 ) x 9 /2 = 135
\(B=\frac{135\cdot1420+45\cdot780\cdot3}{135}\)
\(=\frac{135\cdot1420+135\cdot780}{135}\)
\(=\frac{135\left(1420+780\right)}{135}\)
\(=\frac{135\cdot2200}{135}\)
= 2200

Giusp m với. Tìm số A biết. 121:A dư 10, 61 : A dư 10. giải thích cách làm theo lớp 6 b nhé.Thank

a) =\(\left[\left(12+1\right)^2+\left(12+2\right)^2\right]:\left(13^2+14^2\right)\)
=1
b)=(1.2.3....8).(9-1-8)
=(1.2.3....8).0
=0
mik chỉ giải được zậy thôi.
t mik nha.

\(A=\frac{-5}{7}+\frac{3}{4}+\frac{-1}{5}+\frac{-2}{7}+\frac{1}{4}\)
\(A=\left(\frac{-5}{7}+\frac{-2}{7}\right)+\left(\frac{3}{4}+\frac{1}{4}\right)+\frac{-1}{5}\)
\(A=-1+1+\frac{-1}{5}\)
\(A=\frac{-1}{5}\)
\(B=\frac{-4}{12}+\frac{18}{45}+\frac{-6}{9}+\frac{-21}{35}+\frac{6}{30}\)
\(B=\frac{-1}{3}+\frac{2}{5}+\frac{-2}{3}+\frac{-3}{5}+\frac{1}{5}\)
\(B=\left(\frac{-1}{3}+\frac{-2}{3}\right)+\left(\frac{2}{5}+\frac{-3}{5}+\frac{1}{5}\right)\)
\(B=-1+0\)
\(B=-1\)

A = 3 + 6 + 9 + ... + 2007
=>A = 3( 1 + 2 + 3 + ... + 669 )
=> A = \(3\cdot\left(\frac{670\cdot669}{2}\right)\)
=> A = \(3\cdot224115\)= 672345
B = \(2\cdot53\cdot12+4\cdot6\cdot87-3\cdot8\cdot40\)
=> B = 24 * 53 + 24 * 87 - 24 * 40
=> B = 24 * ( 53 + 87 - 40 )
=> B = 24 * 100 = 2400
c) ta có Tử số = \(2006\cdot\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{2007}\right)\)
Mẫu số = \(\frac{2007-1}{1}\)+\(\frac{2007-2}{2}\)+...+\(\frac{2007-2006}{2006}\)
=> Mẫu số = \(\frac{2007}{1}\)\(-1\)+ \(\frac{2007}{2}\)\(-1\)+ ... + \(\frac{2007}{2006}\)\(-1\)
=> Mẫu số = \(\frac{2007}{1}\)+ \(\frac{2007}{2}\)+ ... + \(\frac{2007}{2006}\)- ( 1 + 1 + 1 + ... + 1 ) ( 1 + 1 + ... + 1 có 2006 số hạng 1 )
=> Mẫu số = ( 2007 - 2006 ) + \(2007\cdot\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2006}\right)\)
=> Mẫu số = \(\frac{2007}{2007}\)+ \(2007\cdot\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2006}\right)\)
=> Mẫu số = \(2007\cdot\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2007}\right)\)
=> C = \(\frac{TS}{MS}\)= \(\frac{2006}{2007}\)

Gợi ý: Sử dụng tính chất phân phối của phép nhân đối với phép cộng để nhóm thừa số chung ra ngoài.
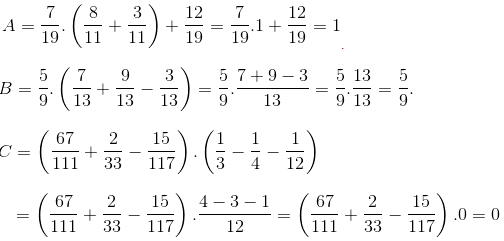
a) 1 3 + − 1 3 + 1 3 = 1 3
b) − 1 3 + 2 5 + − 2 3 + 4 5 = 1 5