Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mãi mãi mới có 1 bài đây nè
Câu hỏi của Nguyễn Thùy Linh - Toán lớp 9 - Học toán với OnlineMath
vào thóng kê
k 3 phát như đã hứa nhé
HHHHHHOOOOCJJJJ TOOOOTS @@

a)Với y=1 ta có hpt:
\(\int^{2x+3=3+m}_{x+2=m}\Leftrightarrow\int^{2x=m}_{x+2=2x}\Leftrightarrow\int^{2.2=m}_{x=2}\Leftrightarrow\int^{m=4}_{x=2}\)
Vậy nghiệm của hpt là (2;1) khi m=4
b)đợi suy nghĩ

Dat \(P=\frac{1}{x^2}+\frac{1}{y^2}\)
\(=\left(\frac{1}{x^2}+4\right)+\left(\frac{1}{y^2}+4\right)-8\ge\frac{4}{x}+\frac{4}{y}-8\ge\frac{16}{x+y}-8=8\)
Dau '=' xay ra khi \(x=y=\frac{1}{2}\)
Vay \(P_{min}=8\)khi \(x=y=\frac{1}{2}\)

1)\(\hept{\begin{cases}\sqrt{x}-\sqrt{x-y-1}=1\\y^2+x+2y\sqrt{x}-y^2x=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(\sqrt{x}-1\right)^2=x-y-1\\\left(y+\sqrt{x}\right)^2-y^2x=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x-2\sqrt{x}+1=x-y-1\\\left(y+\sqrt{x}-y\sqrt{x}\right)\left(y+\sqrt{x}+y\sqrt{x}\right)=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2\sqrt{x}-y=2\\\left(y+\sqrt{x}-y\sqrt{x}\right)\left(y+\sqrt{x}+y\sqrt{x}\right)=0\end{cases}}\)
Đặt \(\hept{\begin{cases}\sqrt{x}=a\left(\ge0\right)\\y=b\end{cases}}\)
=> hệ phương trình \(\Leftrightarrow\hept{\begin{cases}2a-b=2\\\left(b+a-ab\right)\left(b+a+ab\right)=0\end{cases}}\)
Tham khảo nhé~

a) A = B : C = \(\left[\left(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}\right).\frac{2}{\sqrt{x}+\sqrt{y}}+\frac{1}{x}+\frac{1}{y}\right]\). \(\frac{\sqrt{x^3y}+\sqrt{xy^3}}{\sqrt{x^3}+y\sqrt{x}+x\sqrt{y}+\sqrt{y^3}}\)
A xác định <=> x > 0 và y > 0
\(B=\left[\frac{\sqrt{x}+\sqrt{y}}{\sqrt{xy}}.\frac{2}{\sqrt{x}+\sqrt{y}}+\frac{1}{x}+\frac{1}{y}\right]=\frac{2}{\sqrt{xy}}+\frac{1}{x}+\frac{1}{y}=\left(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}\right)^2\)
\(C=\frac{\sqrt{x}.\left(x+y\right)+\sqrt{y}.\left(x+y\right)}{\sqrt{xy}.\left(x+y\right)}=\frac{\left(\sqrt{x}+\sqrt{y}\right).\left(x+y\right)}{\sqrt{xy}.\left(x+y\right)}=\frac{\sqrt{x}+\sqrt{y}}{\sqrt{xy}}=\frac{1}{\sqrt{y}}+\frac{1}{\sqrt{x}}\)
=> A = B : C = \(\left(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}\right)^2\) : \(\left(\frac{1}{\sqrt{y}}+\frac{1}{\sqrt{x}}\right)\) = \(\frac{1}{\sqrt{y}}+\frac{1}{\sqrt{x}}\)
c) \(A=\frac{1}{\sqrt{y}}+\frac{1}{\sqrt{x}}\ge2.\sqrt{\frac{1}{\sqrt{y}}.\frac{1}{\sqrt{x}}}=2.\sqrt{\frac{1}{\sqrt{6}}}\)
=> A nhỏ nhất bằng \(2.\sqrt{\frac{1}{\sqrt{6}}}\) khi \(\frac{1}{\sqrt{y}}=\frac{1}{\sqrt{x}}\) => x = y = \(\sqrt{6}\)

\(D=\frac{2}{\sqrt{xy}}:\left(\frac{1}{\sqrt{x}}-\frac{1}{\sqrt{y}}\right)^2-\frac{x+y}{x-2\sqrt{xy}+y}\left(ĐKXĐ:x\ge0,y\ge0,x\ne y\right)\)
\(\Leftrightarrow D=\frac{2}{\sqrt{xy}}:\left(\frac{\sqrt{y}-\sqrt{x}}{\sqrt{xy}}\right)^2-\frac{x+y}{\sqrt{x}}\)
\(\Leftrightarrow D=\frac{2}{\sqrt{xy}}.\frac{xy}{\left(\sqrt{x}-\sqrt{y}\right)^2}-\frac{x+y}{\left(\sqrt{x}-\sqrt{y}\right)^2}\)
\(\Leftrightarrow D=\frac{2\sqrt{xy}-x-y}{\left(\sqrt{x}-\sqrt{y}\right)^2}=\frac{-\left(\sqrt{x}-\sqrt{y}\right)^2}{\left(\sqrt{x}-\sqrt{y}\right)^2}=-1\)
=> ko phụ thuộc x
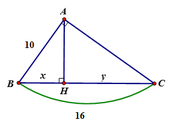
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
A B 2 = B H . B C ⇔ B H = A B 2 B C = 100 16 = 6 , 25 => CH = BC – BH = 16 – 6,25 = 9,75
Vậy x = 6,25; y = 9,75
Đáp án cần chọn là: B