PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 6 2018
a/\(\sqrt{x}=7\)
\(\Leftrightarrow x=49\)
b/\(\Leftrightarrow x< 4\)(do x>0)
\(\Rightarrow x\varepsilon\left\{0;1;2;3\right\}\)
c/\(2x< 16\)
\(\Leftrightarrow x< 8\)
\(\Leftrightarrow x\varepsilon\left\{1;2;3;4;5;6;7\right\}\)
5 tháng 6 2018
a) \(2\sqrt{x}=14\Leftrightarrow\sqrt{x}=7\)
\(\Leftrightarrow x=7^2\Leftrightarrow x=49\)
b) \(\sqrt{x}< \sqrt{2}\Leftrightarrow x< 2\)
c) \(\sqrt{2x}< 4\)
Vì \(4=\sqrt{16}\text{ nên }\sqrt{2x}< 4\text{ có nghĩa là }\sqrt{2x}< 16\)
\(\Leftrightarrow2x< 16\)
\(\Leftrightarrow x< 8\left(x\ge0\right)\)
HT
Hoàng Thị Thu Huyền
Manager
3 tháng 4 2017
Với câu c, Thiên Anh nên thêm điều kiện để phần kết luận là: \(0\le x< 2.\)
NA
1
9 tháng 8 2016
a)\(\sqrt{x}>2\Leftrightarrow\sqrt{x^2}>2^2\Leftrightarrow x>4\)
\(\sqrt{x}< 1\Leftrightarrow\sqrt{x^2}< 1^2\Leftrightarrow x< 1\)
24 tháng 8 2016
a) = 225
b) 49
c) = 1
d) 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7
k nha
24 tháng 8 2016
a) \(\sqrt{x}=15\)
=> x = 152
=> x = 225
b) \(2\sqrt{x}=14\)
<=> \(\sqrt{x}=7\)
=> x = 72
=> x = 49
c) \(\sqrt{x}< \sqrt{2}\)
<=> x < 2
mà \(x\ge0\)
=> x= {0;1}
d) \(\sqrt{2x}< 4\)
=> 2x < 16
<=> x < 8
mà \(x\ge0\)
=> x = {0;1;2;3;4;5;6;7}
ok mk nhé!!!!!! 53654645756876969251353253434645655435436464556756252345345634
NA
4
9 tháng 8 2016
a) \(\sqrt{x}>1\Leftrightarrow x>1\)
b) \(\sqrt{x}< 3\Leftrightarrow x< 9\)
Vì x không âm nên x={0;1;2;3;4;5;6;7;8}
9 tháng 8 2016
a)\(\sqrt{x}>1\Leftrightarrow\sqrt{x^2}>1^2\Leftrightarrow x>1\)
b)\(\sqrt{x}< 3\Leftrightarrow\sqrt{x^2}< 3^2\Leftrightarrow x< 9\)
PL
1
16 tháng 8 2018
\(2\sqrt{x}=14\Rightarrow\sqrt{x}=7\) \(\Rightarrow x=49\)
\(\sqrt{x}< \sqrt{2}\Rightarrow x< 2\) Mà x không âm \(\Rightarrow x\in\left(0;1\right)\)
\(\sqrt{2x}< 4\Rightarrow2x< 16\) \(\Rightarrow x< 8\) mà x không âm \(\Rightarrow x\in\left(0;1;2;3;4;5;6;7\right)\)
NP
1
TH
2
20 tháng 5 2017
Ta có:
\(\sqrt{x}< \sqrt{2}\)
\(\Leftrightarrow x< 2\)
Vì x nguyên không âm nên
\(\Rightarrow1\le x< 2\)
\(\Rightarrow x=1\)
TH
21 tháng 5 2017
\(\sqrt{x}\)<\(\sqrt{2}\)
<=> x<2
vì x nguyên không âm nên
\(\Rightarrow\)0<=x<2
\(\Rightarrow\)x=0;x=1
mà x lớn nhất nên x=1
KB
8 tháng 4 2019
\(B=\frac{ab}{a+b+2}\Rightarrow2B=\frac{2ab}{a+b+2}=\frac{\left(a+b\right)^2-a^2-b^2}{a+b+2}=\frac{\left(a+b\right)^2-4}{a+b+2}=a+b-2\)
Do a ; b không âm , áp dụng BĐT Cô - si cho 2 số , ta có :
\(a+b\le\sqrt{2\left(a^2+b^2\right)}=\sqrt{2.4}=\sqrt{8}\)
\(\Rightarrow a+b-2\le\sqrt{8}-2\)
\(\Rightarrow2B\le\sqrt{8}-2\Rightarrow B\le\sqrt{2}-1\)
Dấu " = " xảy ra \(\Leftrightarrow a=b=\sqrt{2}\)
KB
8 tháng 4 2019
Do x ; y không âm , \(x^2+y^2=1\)
\(\Rightarrow\left|x\right|;\left|y\right|\le1\) \(\Rightarrow0\le x;y\le1\)
\(\Rightarrow x\ge x^2;y\ge y^2\Rightarrow x+y\ge x^2+y^2=1\)
\(x,y\ge0\Rightarrow xy\ge0\)
Ta có : \(A=\sqrt{5x+4}+\sqrt{5y+4}\)
\(\Rightarrow A^2=5x+4+5y+4+2\sqrt{\left(5x+4\right)\left(5y+4\right)}\)
\(=5\left(x+y\right)+8+2\sqrt{25xy+20y+20x+16}\)
\(\ge5.1+8+2\sqrt{25.0+20.1+16}=13+2.6=25\)
\(\Rightarrow A\ge5\)
Dấu " = " xảy ra \(\Leftrightarrow\left[{}\begin{matrix}x=0;y=1\\x=1;y=0\end{matrix}\right.\)
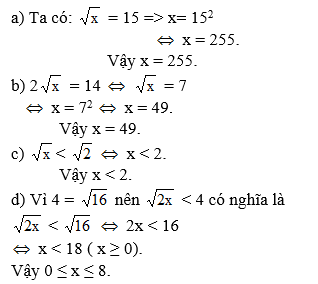
Vì x ≥ 0 nên bình phương hai vế ta được:
2x < 16 ⇔ x < 8
Vậy 0 ≤ x < 8