Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo mình:
để hàm số đồng biến, đk cần là y'=0.
a>0 và \(\Delta'< 0\)
nghịch biến thì a<0
vì denta<0 thì hầm số cùng dấu với a
mình giải được câu a với b
câu c có hai cực trị thì a\(\ne\)0, y'=0, denta>0 (để hàm số có hai nghiệm pb)
câu d dùng viet
câu e mình chưa chắc lắm ^^

Ta có \(f'\left(x\right)=3ax^2+2bx+c;f"\left(x\right)=6ax+2b\)
Hàm số \(f\left(x\right)\) đạt cực tiểu tại \(x=0\) khi và chỉ khi
\(\begin{cases}f'\left(0\right)=0\\f"\left(0\right)>0\end{cases}\)\(\Leftrightarrow\begin{cases}c=0\\2b>0\end{cases}\)\(\Leftrightarrow\begin{cases}c=0\\b>0\end{cases}\left(1\right)\)
Hàm số \(f\left(x\right)\) đạt cực đại tại \(x=1\) khi và chỉ khi \(\begin{cases}f'\left(1\right)=0\\f"\left(1\right)< 0\end{cases}\)\(\Leftrightarrow\begin{cases}3a+2b+c=0\\6a+2b< 0\end{cases}\)
\(\begin{cases}f\left(0\right)=0\\f\left(1\right)=1\end{cases}\)\(\Leftrightarrow\begin{cases}d=0\\a+b+c+d=1\end{cases}\) \(\Leftrightarrow\begin{cases}d=0\\a+b+c+d=1\end{cases}\) (3)
Từ (1), (2), (3) suy ra \(a=-2;b=3;c=0;d=0\)
Kiểm tra lại \(f\left(x\right)=-2x^3+3x^2\)
Ta có \(f'\left(x\right)=-6x^2+6x;f"\left(x\right)=-12x+6\)
\(f"\left(0\right)=6>0\), hàm số đạt cực tiểu tại \(x=0\)
\(f"\left(1\right)=-6< 0\), hàm số đạt cực đại tại \(x=1\)
Vậy \(a=-2;b=3;c=0;d=0\)

Câu 2:
$y'=-3x^2+6x+(m-2)=0$
Để hàm số có 2 điểm cực trị $x_1,x_2$ đồng nghĩa với PT $-3x^2+6x+(m-2)=0$ có 2 nghiệm phân biệt $x_1,x_2$
$\Leftrightarrow \Delta'=9+3(m-2)>0\Leftrightarrow m>-1(1)$
Hai điểm cực trị cùng dương khi:
\(\left\{\begin{matrix} x_1+x_2=2>0\\ x_1x_2=\frac{m-2}{-3}>0\end{matrix}\right.\Leftrightarrow m< 2(2)\)
Từ $(1);(2)\Rightarrow -1< m< 2$
Đáp án C.
Câu 2:
Để đths có 2 điểm cực trị thì trước tiên:
$y'=x^2-2mx+m^2-4=0$ có 2 nghiệm phân biệt $x_1,x_2$
Điều này xảy ra khi $\Delta'=m^2-(m^2-4)>0\Leftrightarrow m\in\mathbb{R}$
Để 2 điểm cực trị của đồ thị $y$ nằm về hai phía của trục tung thì: $x_1x_2< 0$
$\Leftrightarrow m^2-4< 0$
$\Leftrightarrow -2< m< 2$
Đáp án A.

- Ta có \(y'=4x^3-4m^2x;y'=0\) \(\Leftrightarrow\begin{cases}x=0\\x^2=m^2\end{cases}\) Điều kiện có 3 điểm cực trị : \(m\ne0\)
- Tọa độ 3 điểm cực trị : A (0;1); B \(\left(-m;1-m^4\right),C\left(m;1-m^4\right)\)
- Chứng minh tam giác ABC cân đỉnh A. Tọa độ trung điểm I của BC là I \(\left(0;1-m^4\right)\)
- \(S_{ABC}=\frac{1}{2}AI.BC=m^4\left|m\right|=\left|m\right|^5=32\Leftrightarrow m=\pm2\left(tm\right)\)

1.
Hàm trùng phương có đúng 1 cực trị khi:
TH1: \(a=m=0\)
TH2: \(ab=-m>0\Leftrightarrow m< 0\)
\(\Rightarrow m\le0\)
Đáp án B
2.
\(y'=3\left(x^2+2mx+m^2-1\right)=3\left(x+m+1\right)\left(x+m-1\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}x=-m+1\\x=-m-1\end{matrix}\right.\)
Hàm số có 2 cực trị nằm về 2 phía trục hoành
\(\Leftrightarrow y'\left(-m+1\right).y'\left(-m-1\right)< 0\)
\(\Leftrightarrow\left(3m-2\right)\left(3m+2\right)< 0\Rightarrow-\frac{2}{3}< m< \frac{2}{3}\)
\(\Rightarrow a+2b=-\frac{2}{3}+2.\frac{2}{3}=\frac{2}{3}\)
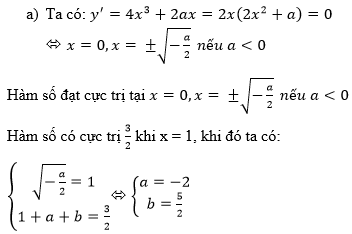

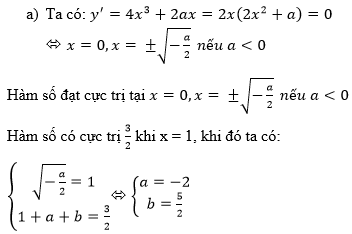
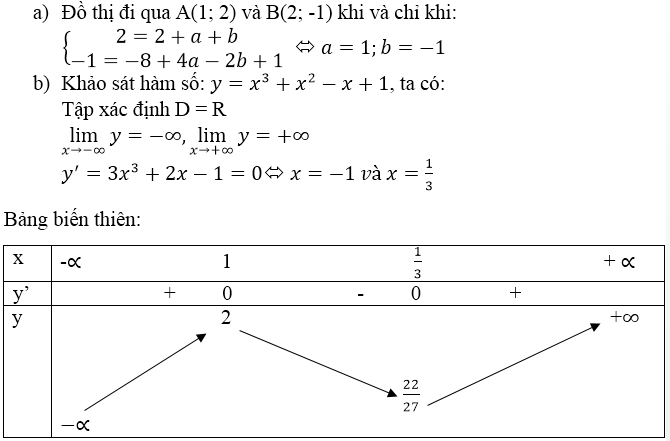
Sử dụng giả thiết và điều kiện cần của cực trị ta có
y(1) = 0; y'(-1) = 0; y(-1) = 0
Trong đó , y ' = 3 x 2 + 2 a x + b
Từ đó suy ra:
Với a = 1; b = -1; c = -1 thì hàm số đã cho trở thành y = x 3 + x 2 - x - 1
Ta có y ' = 3 x 2 + 2 x - 1 , y ' ' = 6 x + 2 . V ì y ' ' = ( - 1 ) = - 4 < 0 nên hàm số đạt cực đại tại x = -1 . Vậy a = 1; b = -1; c = -1 là các giá trị cần tìm.
Chọn đáp án C.