Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a)
Dễ thấy \(IA=IB=R(I); KA=KB=R(K)\) nên tam giác \(IAB; KAC\) là tam giác cân.
Áp dụng tính chất tam giác cân và tính chất tiếp tuyến: \(\widehat{IAB}=\widehat{IBA}=\widehat{IBC}-\widehat{ABC}=90^0-\widehat{ABC}\)
\(\widehat{KAC}=\widehat{KCA}=\widehat{KCB}-\widehat{ACB}=90^0-\widehat{ACB}\)
\(\Rightarrow \widehat{IAB}+\widehat{KAC}=180^0-(\widehat{ABC}+\widehat{ACB})\)
\(\Leftrightarrow \widehat{IAB}+\widehat{KAC}=180^0-90^0=90^0\)
\(\Leftrightarrow \widehat{IAK}=90^0+\widehat{BAC}=90^0+90^0=180^0\)
\(\Rightarrow I,A,K\) thẳng hàng.
Hai đường tròn (I); (K) giao nhau tại A và I,A,K thẳng hàng nên IA+AK=IK nên (I) và (K) tiếp xúc với nhau tại A.
b)
Tam giác BAC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền nên \(AM=\frac{BC}{2}=BM\Rightarrow \triangle MAB\) cân tại M
\(\Rightarrow \widehat{MAB}=\widehat{MBA}=\widehat{CBA}=90^0-\widehat{IBA}=90^0-\widehat{IAB}\)
\(\Rightarrow \widehat{IAM}=\widehat{MAB}+\widehat{IAB}=90^0\Rightarrow IA\perp AM\) nên AM là tiếp tuyến của (I)
Hoàn toàn tương tự ta có AM là tiếp tuyến của (K)
Ta có đpcm.

Bài 2:
Xét ΔOAB vuông tại B có
\(OA^2=OB^2+AB^2\)
hay AB=8(cm)

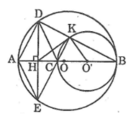
Vì O, O’ và B thẳng hàng nên: O’B < OB => O’ nằm giữa O và B
Ta có: OO’ = OB - O’B
Vậy đường tròn (O’) tiếp xúc với đường tròn (O) tại B

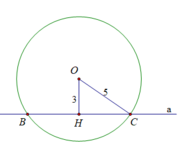
a) Đường thẳng a cắt đường tròn (O) tại 2 điểm phân biệt, vì khoảng cách d < R
b) Xét tam giác OHC vuông tại H có:
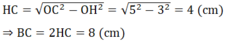



- Tiếp điểm của hai đường tròn tiếp xúc với nhau thì nằm trên đường nối tâm.
- Các giao điểm của hai đường tròn cắt nhau thì đối xứng với nhau qua đường nối tâm.