Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

C2H2 + 2AgNO3 + 2NH3 → C2Ag2 ↓ + 2NH4NO3
CH3CHO + 2AgNO3 + 3NH3 + H2O → CH3COONH4 + 2Ag ↓ + 2NH4NO3
C2Ag2 + 2HCl → 2AgCl ↓ + C2H2 ↑
Y(AgCl, Ag) + HNO3 --> ...
Ag + 2HNO3 → AgNO3 + NO2 ↑ + H2O

Câu trả lời của bạn Vũ Thị Ngọc Chinh câu a và câu b tớ thấy đúng rồi, ccâu c ý tính năng lượng của photon ứng với vạch giới hạn của dãy paschen tớ tính thế này:
Khi chuyển từ mức năng lượng cao \(E_{n'}\)về mức năng lượng thấp hơn \(E_n\)năng lượng của e giảm đi một lượng đứng bằng năng lượng cảu một photon nên trong trương hợp này đối vs nguyên tử H thì nang lượng photon ứng với vạch giới hạn của dãy paschen là:
\(\Delta E=E_{n'}-E_n=\left(0-\left(-13,6.\frac{1}{n^2}\right)\right)=13,6.\frac{1}{3^2}=1.51\left(eV\right)\)
Không biết đúng không có gì sai góp ý nhé!!
a. pt S ở trạng thái dừng:
\(\bigtriangledown\)2\(\Psi\)+\(\frac{8m\pi^2}{h^2}\)(E-U)\(\Psi\)=0
đối với Hidro và các ion giống nó, thế năng tương tác hút giữa e và hạt nhân:
U=-\(\frac{Z^2_e}{r}\)
\(\rightarrow\)pt Schrodinger của nguyên tử Hidro và các ion giống nó:
\(\bigtriangledown\)2\(\Psi\)+\(\frac{8m\pi^2}{h^2}\)(E+\(\frac{Z^2_e}{r}\))=0
b.Số sóng : \(\widetilde{\nu}\)=\(\frac{1}{\lambda}\)=\(\frac{1}{4861,3.10^{-10}}\)
ta có : \(\widetilde{\nu}\)=Rh.(\(\frac{1}{n^2}\)-\(\frac{1}{n'^2}\)
\(\rightarrow\)Hằng số Rydberg:
Rh=\(\frac{\widetilde{v}}{\frac{1}{n^2}-\frac{1}{n'^2}}\)=\(\frac{1}{\lambda.\left(\frac{1}{n^2}-\frac{1}{n'^2}\right)}\)
vạch màu lam:n=3 ; n'=4
Rh=\(\frac{1}{4861,3.10^{-10}.\left(\frac{1}{2^2}-\frac{1}{4^2}\right)}\)=10971.103 m-1=109710 cm-1.
c.Dãy Paschen :vạch phổ đầu tiên n=3 ; vạch phổ giới hạn n'=\(\infty\)
Số sóng : \(\widetilde{\nu}\)= Rh.(\(\frac{1}{n^2}\)-\(\frac{1}{n'^2}\))
=109710.(\(\frac{1}{3^2}\)-\(\frac{1}{\infty^2}\))=12190 cm-1.
Năng lượng của photon ứng với vạch giới hạn của dãy Paschen:
En=-13,6.\(\frac{1}{n^2}\)=-13,6.\(\frac{1}{\infty}\)=0.

nZn = mol, nS =
mol.
Phương trình hóa học của phản ứng:
Zn + S -> ZnS
0,07 0,07 0,07 (mol)
Khối lượng các chất sau phản ứng:
mZn(dư) = (0,01 -0,007).65 = 0,195 gam.
mZnS = 0,007.97 = 0,679g.

Ta có hệ thức De_Broglie: λ= h/m.chmc
Đối với vật thể có khối lượng m và vận tốc v ta có: λ= h/m.vhmv
a) Ta có m=1g=10-3kg và v=1,0 cm/s=10-2m/s
→ λ= 6,625.10−3410−3.10−2=6,625.10-29 (m)
b) Ta có m=1g=10-3kg và v =100 km/s=105 m
→ λ= 6,625.10−3410−3.105= 6,625.10-36 (m)
c) Ta có mHe=4,003 = 4,003. 1,66.10-24. 10-3=6,645.10-27 kg và v= 1000m/s
→ λ= 6,625.10−344,03.1000=9.97.10-11 (m)
a) áp dụng công thức
\(\lambda=\frac{h}{mv}=\frac{6,625.10^{-34}}{10^{-3}.10^{-2}}=6,625.10^{-29}\left(m\right)\)
b)
\(\lambda=\frac{6,625.10^{-34}}{10^{-3}.100.10^3}=6,625.10^{-36}\left(m\right)\)
c)
\(\lambda=\frac{6,625.10^{-34}}{4,003.1000}=1,65.10^{-37}\left(m\right)\)

Ta có: cos 450 = \(\frac{\text{ λ}}{\text{ λ}'}=\frac{\text{ λ}}{0,22}\)
=> λ = cos450.0,22 = 0.156Ǻ
Thưa thầy, thầy chữa bài này được không ạ. Thầy ra lâu rồi nhưng chưa có đáp án đúng

Câu a:
+ Dẫn mẫu thử các khí trên qua dd \(Ca\left(OH\right)_2\), khí nào tạo kết tủa với dd này là\(CO_2\):
\(CO_2+Ca\left(OH\right)_2\rightarrow CaCO_3\downarrow+H_2O\)
+ 3 khí còn lại dẫn qua ống nghiệm nằm ngang có chứa bột \(CuO\), đun nóng.
\(\rightarrow\) Khí nào làm bột \(CuO\) từ màu đen sang màu đỏ (do xuất hiện Cu) và có hơi nước thoát ra là \(H_2\):
\(H_2+CuO\underrightarrow{t^o}Cu+H_2O\)
+ 2 khí còn lại:
Cho mẫu than đang cháy dở vào:
\(\rightarrow\) Mẫu than bùng cháy: \(O_2\):
\(C+O_2\underrightarrow{t^o}CO_2\)
\(\rightarrow\) Còn lại là \(H_2\)
Câu b:
Có 3 chất bột \(CaO,CaCO_3,P_2O_5\)
Cho quỳ tím ẩm vào (là quỳ tím có chứa nước)
\(\rightarrow\) Quỳ ẩm chuyển xanh: \(CaO\)
\(CaO+H_2O\rightarrow Ca\left(OH\right)_2\) (nước có trong quỳ, \(Ca\left(OH\right)_2\) làm chuyển xanh)
\(\rightarrow\) Quỳ ẩm chuyển đỏ: \(P_2O_5\)
\(P_2O_5+3H_2O\rightarrow2H_3PO_4\) (nước có trong quỳ, \(H_3PO_4\) làm chuyển đỏ)
\(\rightarrow\) Còn lại là \(CaCO_3\)

phương trình dạng toán tử : \(\widehat{H}\)\(\Psi\) = E\(\Psi\)
Toán tử Laplace: \(\bigtriangledown\)2 = \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\)
thay vào từng bài cụ thể ta có :
a.sin(x+y+z)
\(\bigtriangledown\)2 f(x,y,z) = ( \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\))sin(x+y+z)
=\(\frac{\partial^2}{\partial x^2}\)sin(x+y+z) + \(\frac{\partial^2}{\partial y^2}\)sin(x+y+z) + \(\frac{\partial^2}{\partial z^2}\)sin(x+y+z)
=\(\frac{\partial}{\partial x}\)cos(x+y+z) + \(\frac{\partial}{\partial y}\)cos(x+y+z) + \(\frac{\partial}{\partial z}\)cos(x+y+z)
= -3.sin(x+y+z)
\(\Rightarrow\) sin(x+y+z) là hàm riêng. với trị riêng bằng -3.
b.cos(xy+yz+zx)
\(\bigtriangledown\)2 f(x,y,z) = ( \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\))cos(xy+yz+zx)
=\(\frac{\partial^2}{\partial x^2}\)cos(xy+yz+zx) +\(\frac{\partial^2}{\partial y^2}\)cos(xy+yz+zx) + \(\frac{\partial^2}{\partial z^2}\)cos(xy+yz+zx)
=\(\frac{\partial}{\partial x}\)(y+z).-sin(xy+yz+zx) + \(\frac{\partial}{\partial y}\)(x+z).-sin(xy+yz+zx) + \(\frac{\partial}{\partial z}\)(y+x).-sin(xy+yz+zx)
=- ((y+z)2cos(xy+yz+zx) + (x+z)2cos(xy+yz+zx) + (y+x)2cos(xy+yz+zx))
=-((y+z)2+ (x+z)2 + (x+z)2).cos(xy+yz+zx)
\(\Rightarrow\) cos(xy+yz+zx) không là hàm riêng của toán tử laplace.
c.exp(x2+y2+z2)

chộ cái mặt nhà mi là biết rồi , vào trang chủ của tau rồi bấm theo dõi đi
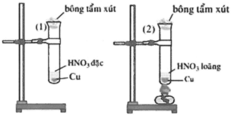
Đáp án D
Ở thí nghiệm (1) Cu + HNO3 đặc tạo thành dung dịch đồng (II) nitrat có màu xanh đồng thời thoát ra khí NO2 có màu nâu đỏ. Ở thí nghiệm (2) Cu + HNO3 loãng tạo thành dung dịch đồng (II) nitrat có màu xanh đồng thời thoát ra khí NO không màu, khi gặp không khí khí NO bị oxi hóa tạo thành NO2 có màu nâu đỏ.