Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

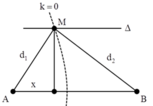
A,B là 2 nguồn cùng pha nên đường trung trực của AB dao động cực đại.
Giữa M và đường trung trực của AB có 3 dãy dực đại khác => M nằm trên dãy cực đại k = 4
\(d_2-d_1=(k+\frac{\triangle\varphi}{2\pi})\lambda = (4+0)\lambda \Rightarrow \lambda = \frac{d_2-d_1}{4}=\frac{21-19}{4}=0.5cm \Rightarrow v = f.\lambda = 80.0,5=40cm/s.\)

Gọi hình chiếu của điểm M trên AB là N, trung điểm của AB là O, đặt ON = x \(\Rightarrow\) \(AM=\sqrt{4+\left(4-x\right)^2}\)\(,BM=\sqrt{4+\left(4+x\right)^2}\)
\(\vartheta BM=\frac{2\pi BM}{\lambda}\)
\(\vartheta AM=\frac{2\pi AM}{\lambda}\)
\(\Rightarrow\frac{2\pi}{\lambda}\left(MB-MA\right)=\left(2k+1\right)\lambda\pi\)
Min khi k = 0 \(\Leftrightarrow\sqrt{4+\left(4+x\right)^2}-\sqrt{4+\left(4-x\right)^2}\)\(=1\Rightarrow x\approx0,56\left(cm\right)\)
chọn đáp án A

Đáp án A
+ Tần số góc của khung dây ω = 2 πn = 2 π . 50 = 100 π rad / s rad/s
→ Suất điện động cảm ứng cực đại
E 0 = ωNBS = 100 π . 500 . 2 5 π . 220 . 10 - 4 = 220 2 V .

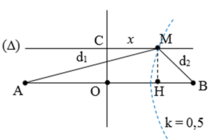
+ Để M là cực tiểu và gần trung trực của của AB nhất thì M phải nằm trên cực tiểu ứng với k = 0.
→ d2 – d1 = (0 + 0,5)λ = 1 cm.
Từ hình vẽ, ta có:
d 1 2 = 2 2 + x 2 d 2 2 = 2 2 + 8 − x 2 → 2 2 + 8 − x 2 − 2 2 + x 2 = 1
→ Giải phương trình trên ta thu được x = 3,44 cm.
Vậy khoảng cách ngắn nhất giữa M và trung trực AB là 4 – 3,44 = 0,56 cm.
Đáp án A

A B P d M d x d1 d2
\(d_1 - d_2 = \left( {\phi _m - \phi } \right)\dfrac{\lambda }{{2\pi }} = \left( {2k + 1} \right)\dfrac{{0.5\pi }}{{2\pi }} = \dfrac{k}{2} + 0.25 \)
Điểm M gần hất \(\Rightarrow k = 0 \Rightarrow d_1 - d_2 = 0.25 \)
\(\Rightarrow \sqrt {(\dfrac{d}{2} + x)^2 + 100^2 } - \sqrt {(\dfrac{d}{2} - x)^2 + 100^2 } = 0.25 \)
\(\Rightarrow \sqrt {(\dfrac{1}{2} + x)^2 + 100^2 } - \sqrt {(\dfrac{1}{2} - x)^2 + 100^2 } = 0.25 \)
\(\Rightarrow x = 25.82 m\)


Đáp án D
+ Số dãy cực đại trên đoạn
+ Để CM là lớn nhất thì M thuộc hypebol ứng với k=2
Ta có d 1 - d 2 = 8 cm
+ Với: